
왠지 이름만 들어도 어려울 것 같은 느낌이 팍팍 드는, Dynamic Programming !!!
연구비를 타내기 위해 그냥 있어보이려고 멋지게 작명하다보니 이런 이름을 가졌다고 한다.
사람 사는게 다 그렇지 뭐~ ^^
"Dynamic Programming"은 뭔가 계산하는 알고리즘이라기 보다는
작은 문제를 풀어서 그 중간 결과를 기록해 놓음으로써 다시 재계산하지 않도록 하는 방법이다.
여러 유형의 문제를 Dynamic Programming으로 푸는 것을 살펴볼텐데
그 첫번째로 살펴볼 것이 바로 "Assembly-line scheduling" 이다.
[Definition]
'Assembly-line'이라는 것에 대한 정의 부터 살펴보자.

컨베이어벨트를 따라 단계별로 부품 조립하는 것을 생각하면 된다.
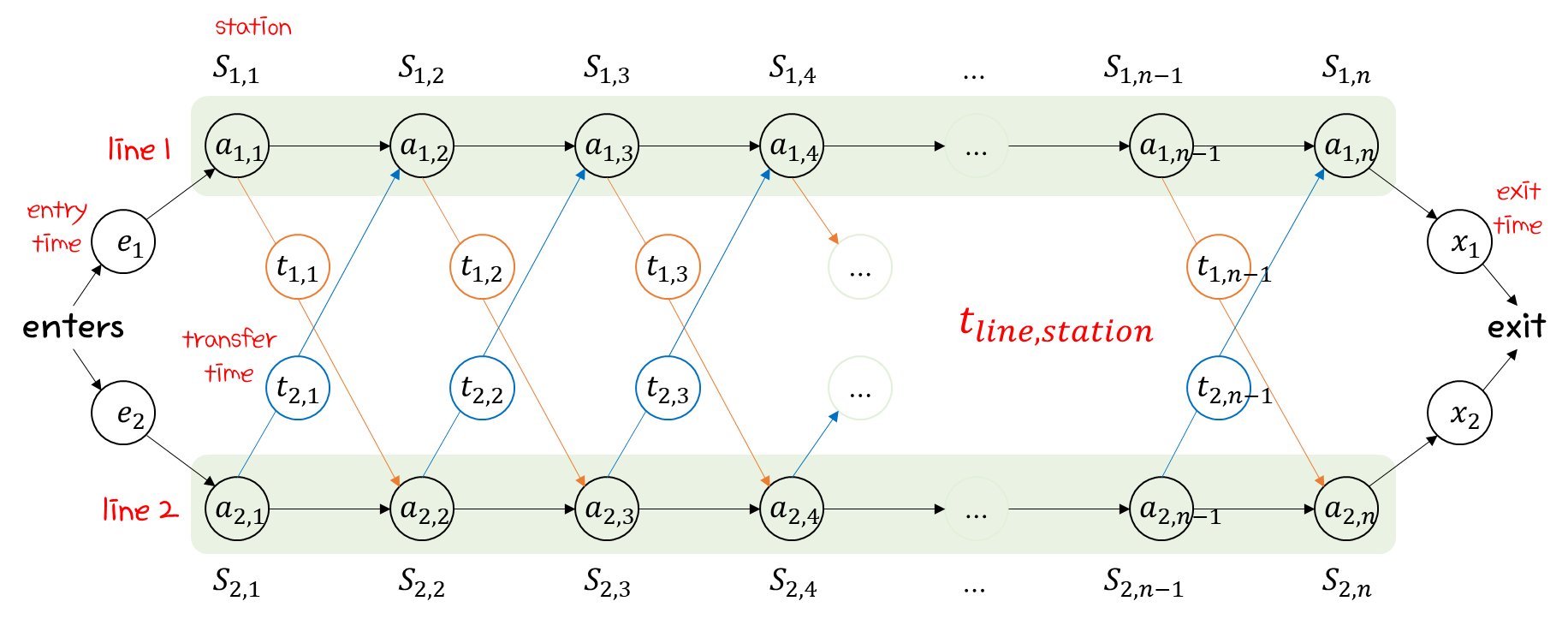
- station : 조립 단계. 제품 조립은 n개의 station을 거치면 완성이 된다.
- a : 각 station 단계에서 소요되는 시간
- line : 하나의 컨베이어 벨트로 생각하면 된다.
- e : line에 조립을 시작하도록 하기 위해 소요되는 시간
- x : 조립 완료된 제품을 전달하기 위해 소요되는 시간
- t : line을 옮기기 위해 소요되는 시간
[Problem]
여러 line으로 구성된 assembly-line이 있을 때,
어떤 경로가 가장 짧은 소요 시간으로 조립할 수 있는지 최적의(가장 빠른) 경로를 찾는 방법은?
[Solution-1]
가장 확실하고 무식한(?) 방법으 모든 경우의 수를 구해서 찾는 방법이다.
하지만, 말 그대로 무식한 방법이기에 ... 경우의 수가 너무 크다.
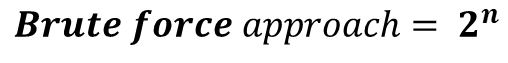
[Solution-2]
스마트한 방법을 찾아보자.
▷ Idea
어느 시점(S)에서 자기 순서까지 올 수 있는 방법은 2가지 경우 밖에 없다.
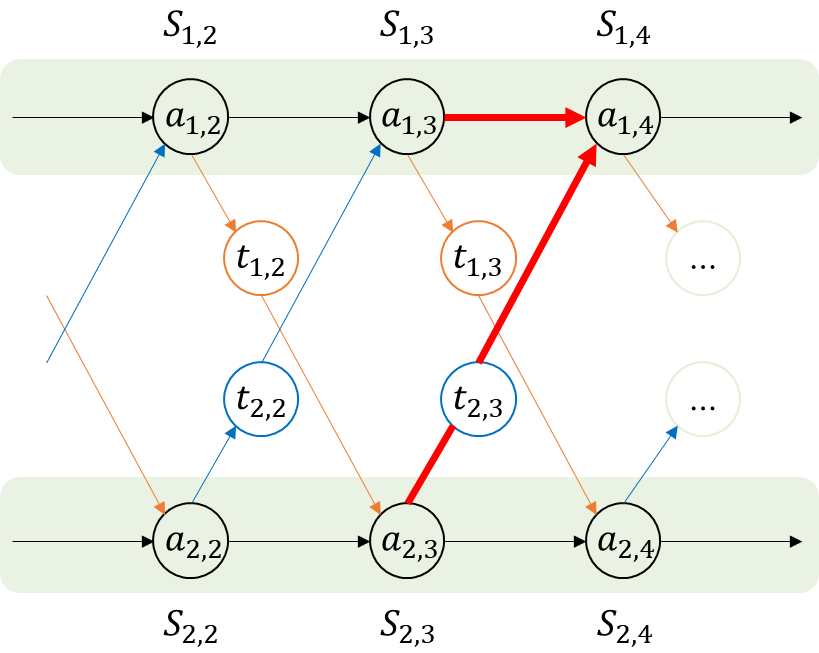
자기가 있는 동일한 line의 직전 단계에서 오는 방법과, 다른 line의 직전 단계에서 오는 2가지의 경우이다.
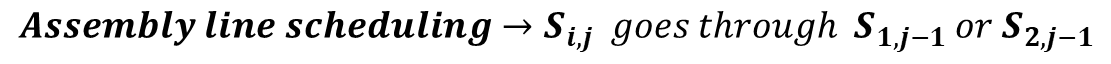
그러면, 그 2가지의 경우 중에 가장 빠른 것을 선택하면 되게 되는 것이다.
▷ How to
그러면 예시를 살펴보자.
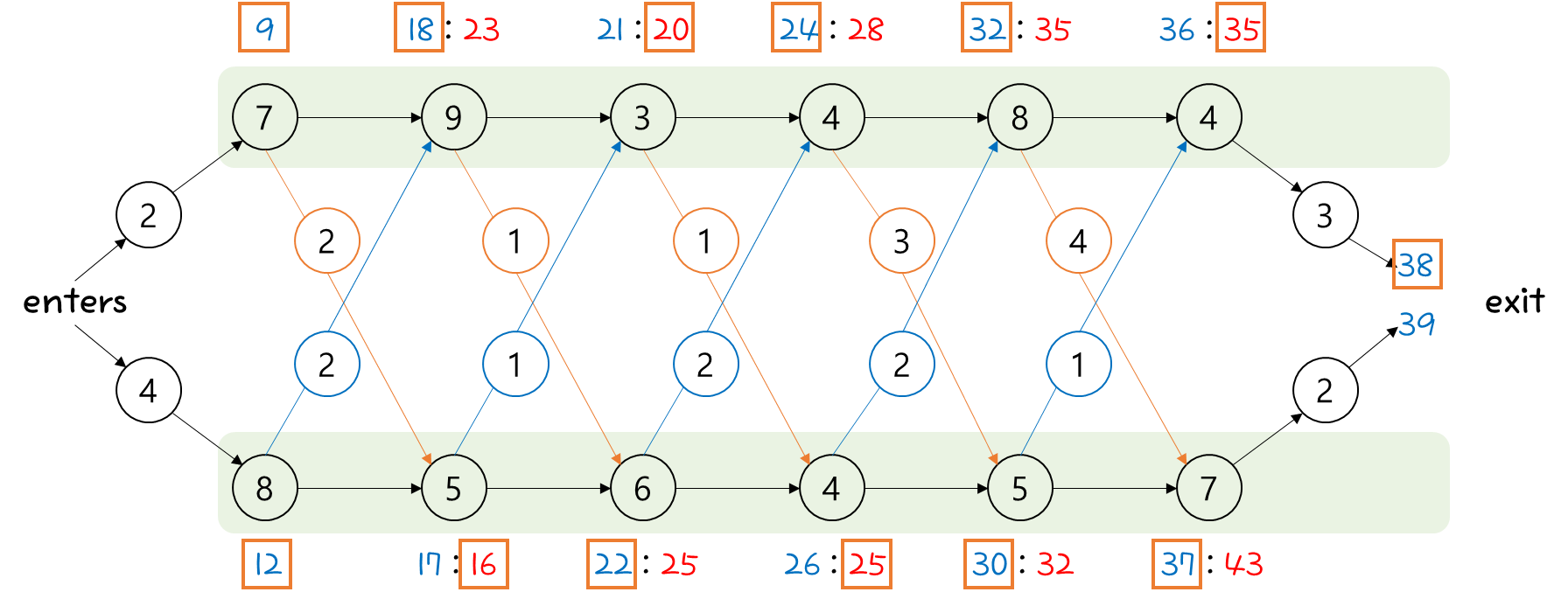
각 단계에서 소요되는 시간을 더해가면서 정리하면 된다.
보다 더 짧은 시간을 선택하면 되기 때문에 □로 표기된 값들이 선택된 결과들이다.
이렇게 선택하는 과정에서 소요되는 Running Time은 어떻게 될까?
각 Station에서 2개씩 값을 보면 되기 때문에 2n의 Running Time이 필요하고,
entry + exit 과정이 있기 때문에 이를 정리하면 다음과 같다.

Brute-force 방법으로 할 때에는 어느 시점(S)에서 자기한테 까지 오는 모든 경우의 수를 살펴보지만
지금 방식에서는 바로 직전의 2가지 경우만 살펴보기 때문에 n에 비례하는 복잡도를 갖게 되었다.
그러면, 중간에 각 S단계에 따른 값들을 어떻게 저장하면 될까?

위와 같은 표 내용만 기록/기억 하고 있으면 되는 것이다.
그런데, 이 것만 가지고는 어떤 경로로 구성된 것인지 알기가 어렵다.
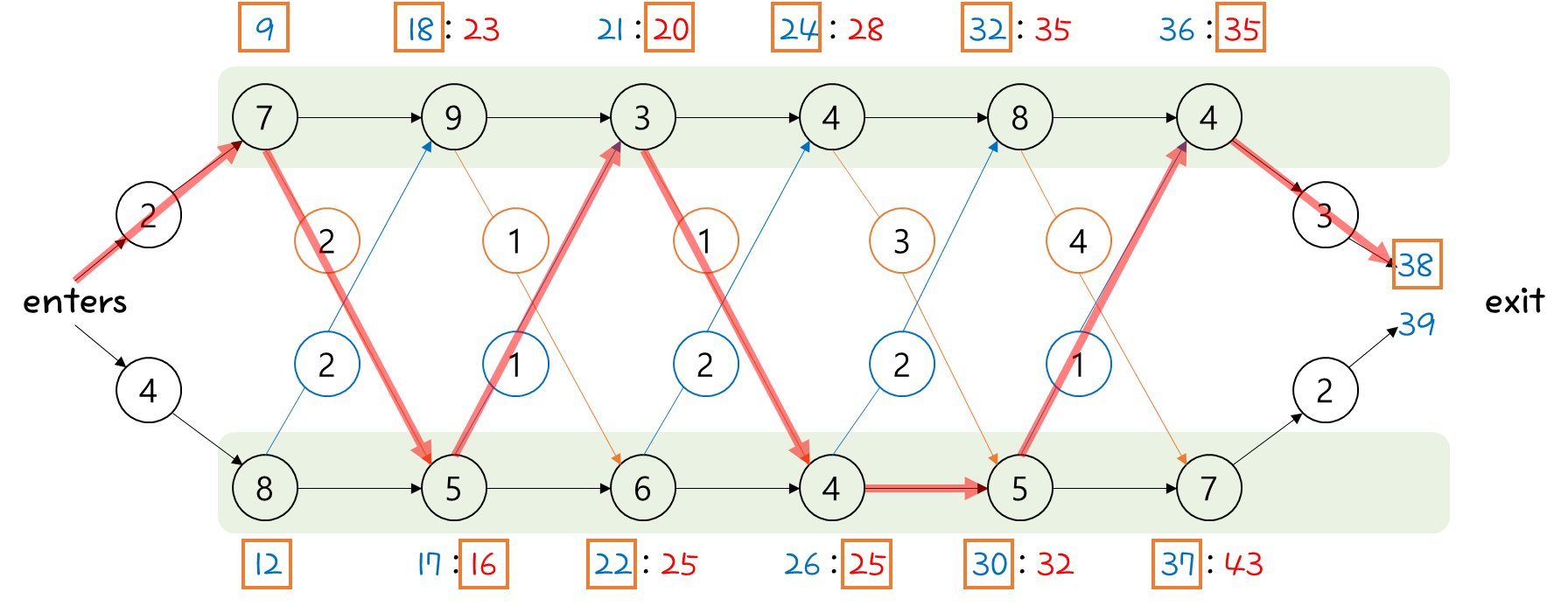
이 내용을 기록할 표가 하나 더 필요한 것이다.

그런데, 2개의 테이블이 모두 필요할까?
경로만 확인 가능해도 되는 경우에는 L table만 있으면 된다.
S table은 현재 값과 직전 값만 알면 되고, 최적해(S* = 38) 값만 저장하면 된다.
S table에서 S3를 계산할 때 S2 값만 알면 된다. 즉, S1의 내용은 필요 없다.
메모리를 굳이 table 전체 크기만큼 잡아 놓지 않아도 된다는 것이다.

L table 값만 알면 최적 경로를 찾을 수 있기 때문이다.
반대로 S 값을 갖고 있는 table만 있어도 L 값 table 없이 경로를 찾아낼 수는 있다.
하지만 L 값 table을 사용하는 것이 훨씬 더 편하기에 L Table을 이용하는 것이다.
▷ Pseudo Code
코드로 구현해보면 다음과 같다.

뭔가 복잡해보이는데, 살펴보기 편하게 구분해보면 다음과 같다.

결과를 출력하는 부분은 아래와 같이 구현해볼 수 있다.
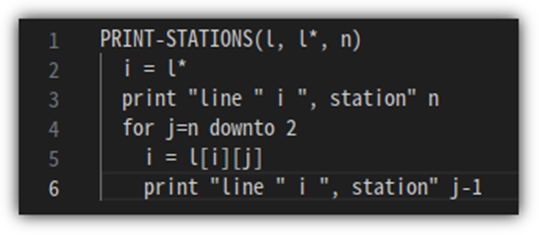
실행 결과는 다음과 같이 나올 것이다.

▷ Space consumption
일단 기본적으로는 S table과 L table 모두 필요로 한다는 전제 하에 다음과 같은 메모리 사용량을 필요로 한다.
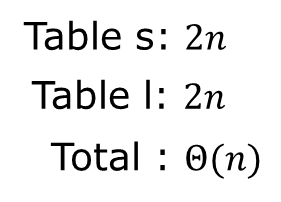
▷ Running time
하나의 요소 別 소요 시간이 Θ(1) 소요시간이 걸린다고 했을 때, 전체 소요 시간은 Θ(n)이라고 할 수 있다.

뭔가 심오한 Dynamic Programming의 세계이다~
'Programming > Algorithm' 카테고리의 다른 글
| 알고리즘 #2 - Dynamic Programming #3 - Longest-Common-Subsequence #1 (0) | 2024.03.25 |
|---|---|
| 알고리즘 #2 - Dynamic Programming #2 - Rod-Cutting #1 (0) | 2024.03.09 |
| 알고리즘 #1 - 정렬 문제 #8 - Radix Sort #1 (1) | 2024.02.21 |
| 알고리즘 #1 - 정렬 문제 #7 - Counting Sort #1 (0) | 2024.02.21 |
| 알고리즘 #1 - 정렬 문제 #6 - Lower bounds #1 (0) | 2024.02.20 |