
이번에 살펴볼 것은 한글로 말하자면, "막대 자르기" 알고리즘이다.
어떤 문제를 해결하기 위한 알고리즘인지 알아보자.
[Problem]
n만큼의 길이를 갖고 있는 막대기가 있다고 하자.
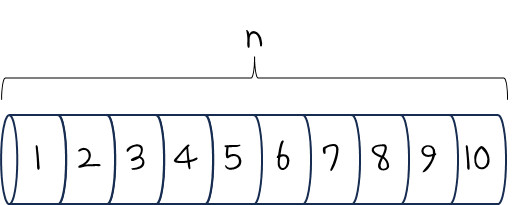
이 막대기를 잘라서 팔아야 하는데, 길이에 따라서 판매되는 가격이 다르다고 했을 때
어떻게 잘라서 팔아야 최대 이익이 나오는지를 찾아내야 하는 것이 문제이다.

위와 같이 막대기 길이에 따른 수익은 제시가 된다.
알아야 할 notation 규칙은 다음과 같다.

[Brute force approach]
"n = 4" 만큼의 길이를 갖고 있는 막대기가 있고, 길이에 따른 가격은 다음과 같다.

이 때, 나올 수 있는 모든 경우의 수를 다 살펴보자면 다음과 같다.
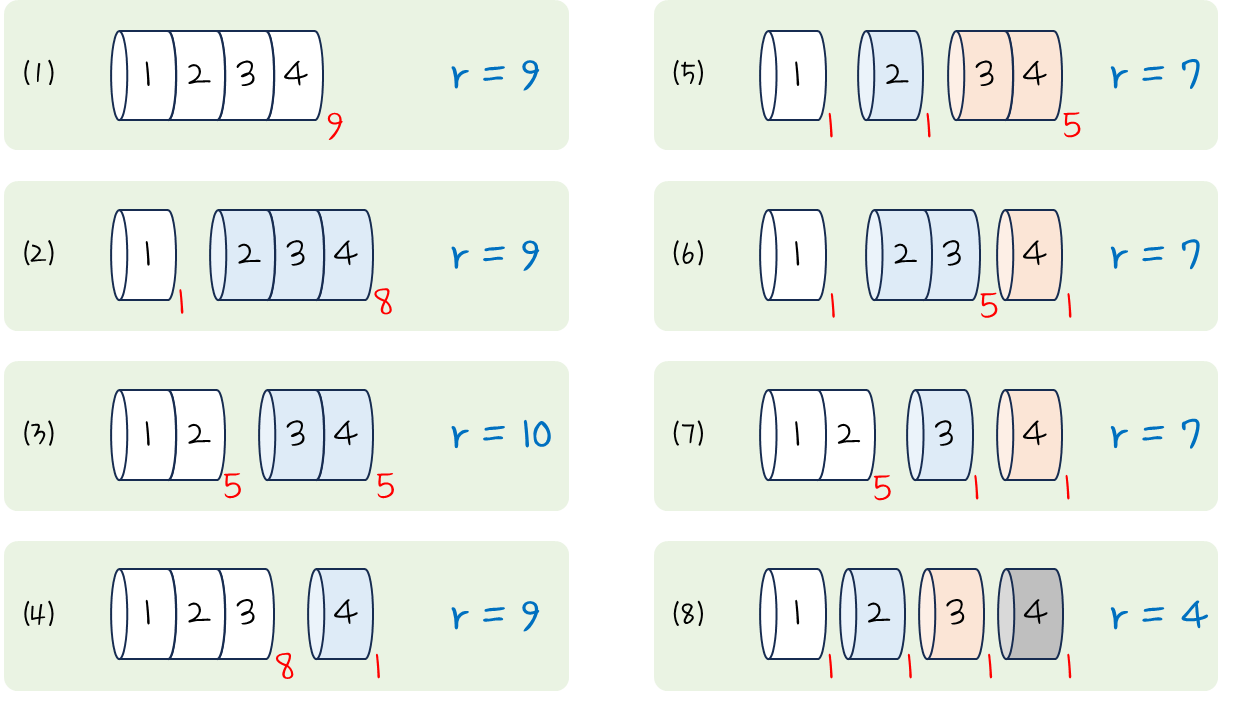
최대 수익을 얻기 위해서는 ⑶번과 같이 2개 묶음으로 나누는 경우가 10만큼의 수익을 얻을 수 있다.
그런데, 이처럼 모든 경우의 수를 나열해서 모두 계산해보기에는 너무 비효율적이다.
[Rod-Cutting Algorithm]
일단 다음과 같은 계산식을 살펴보자.
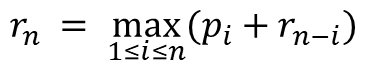
n 길이의 막대기가 있을 때, i 길이의 가격과 'n - i' 길이일 때의 최대 수익의 합이 최대인 i값을 찾는 것을 의미 한다.

다음과 같은 문제가 주어졌다고 해보자.
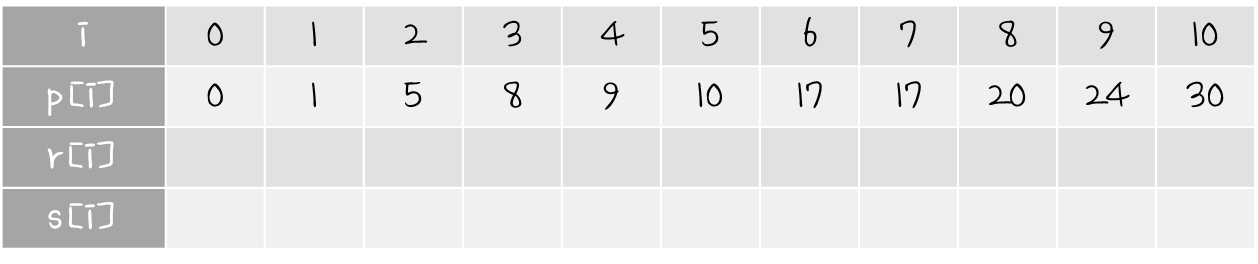
r[i], s[i] 값은 다음과 같이 계산해볼 수 있다.
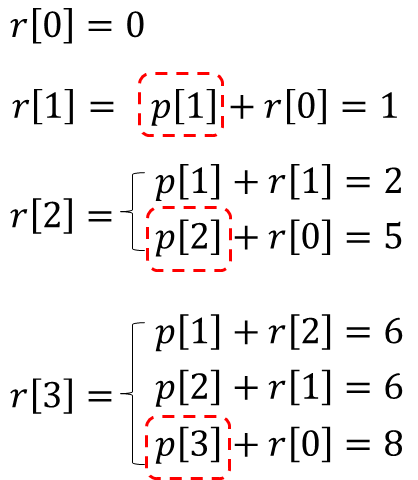
그러면 다음과 같은 결과를 얻을 수 있다.

이렇게 만들어진 표가 있다면,
8 길이만큼의 막대기가 주어졌을 때 다음과 같이 활용할 수 있다.

[Pseudo Code]
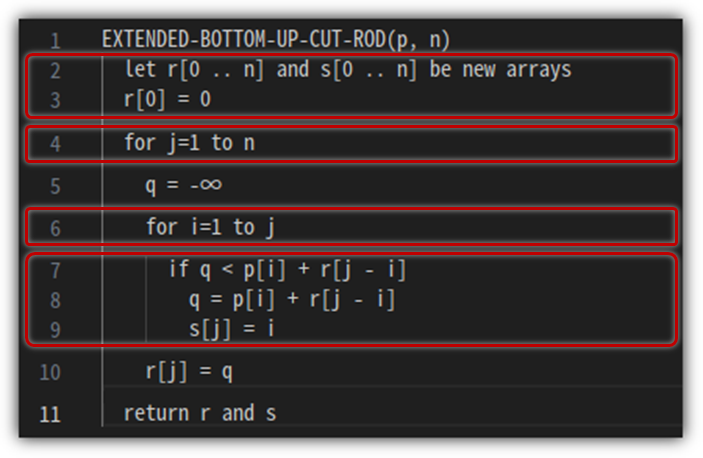
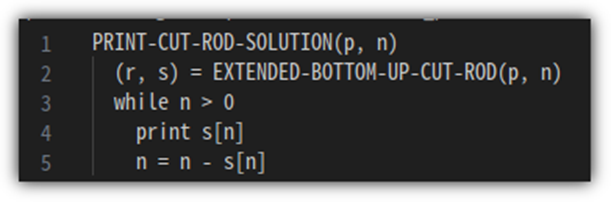
[Time & Space]
이 알고리즘에서는 r[n], s[n] 값을 저장하기 위한 메모리 공간을 필요로 한다.
길이 n 값에 선형으로 비례하는 만큼 사용하기 때문에 다음과 같이 정리할 수 있다.

소요 시간은 Pseudo Code를 보면 중복 for문이 사용되는 부분을 잘 살펴봐야 하는데,
다음과 같이 정리 해볼 수 있다.

수고하셨습니다 !!!
'Programming > Algorithm' 카테고리의 다른 글
| 알고리즘 #2 - Dynamic Programming #4 - Matrix-Chain Multiplication #1 (0) | 2024.04.07 |
|---|---|
| 알고리즘 #2 - Dynamic Programming #3 - Longest-Common-Subsequence #1 (0) | 2024.03.25 |
| 알고리즘 #2 - Dynamic Programming #1 - Assembly-line scheduling #1 (0) | 2024.02.28 |
| 알고리즘 #1 - 정렬 문제 #8 - Radix Sort #1 (1) | 2024.02.21 |
| 알고리즘 #1 - 정렬 문제 #7 - Counting Sort #1 (0) | 2024.02.21 |