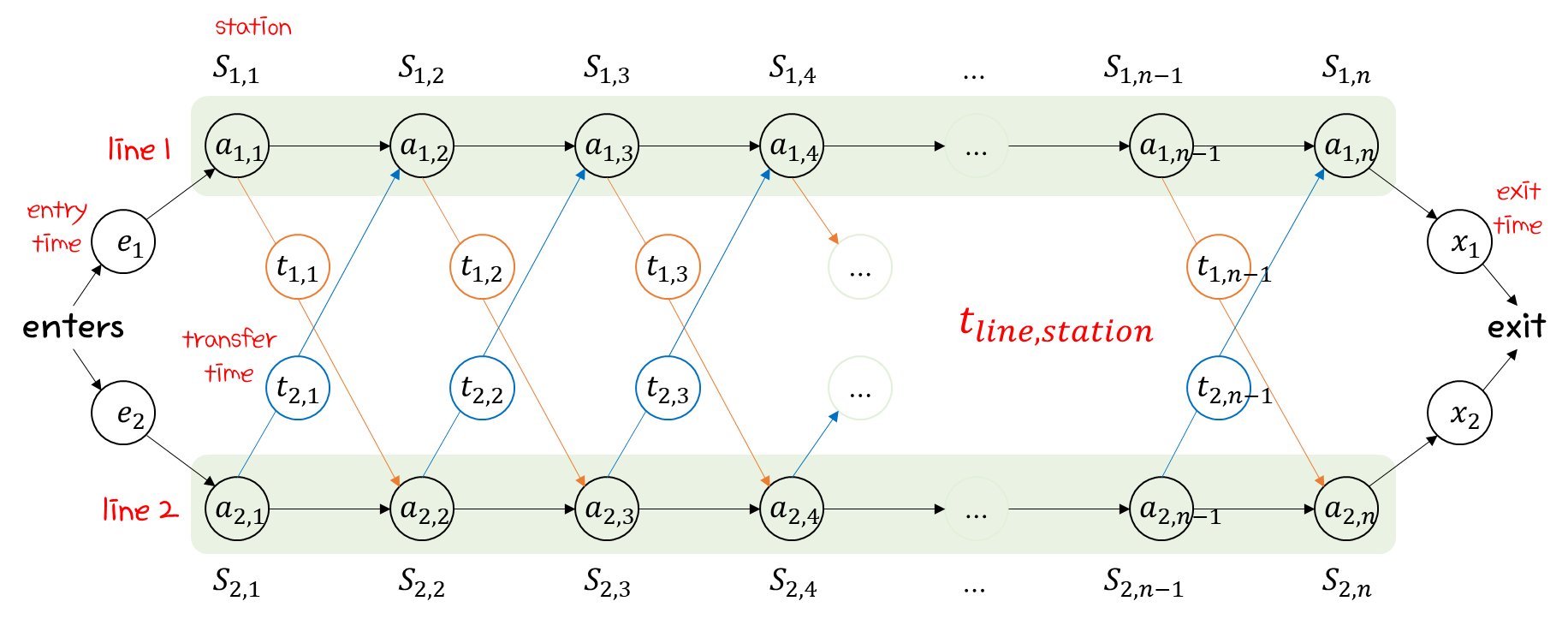
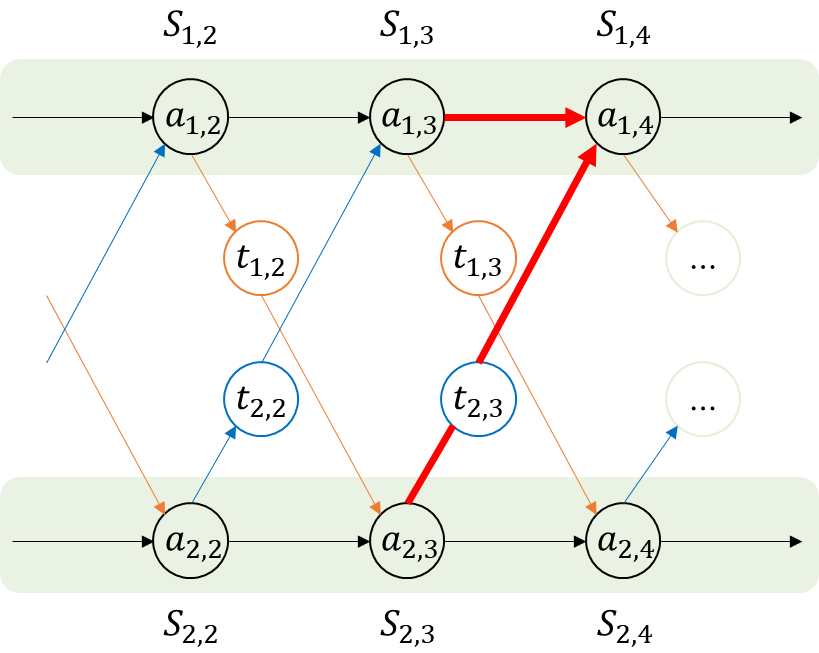
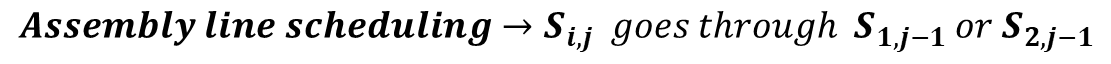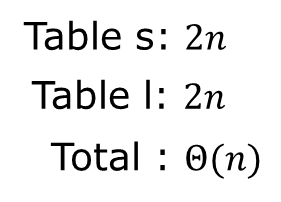이번에 살펴볼 Dynamin Programming 알고리즘은
Matrix-Chain Multiplication (연쇄 행렬 곱셈)이다.
[Background]
우선 알아야할 내용은 바로 "행렬 곱" 규칙이다.
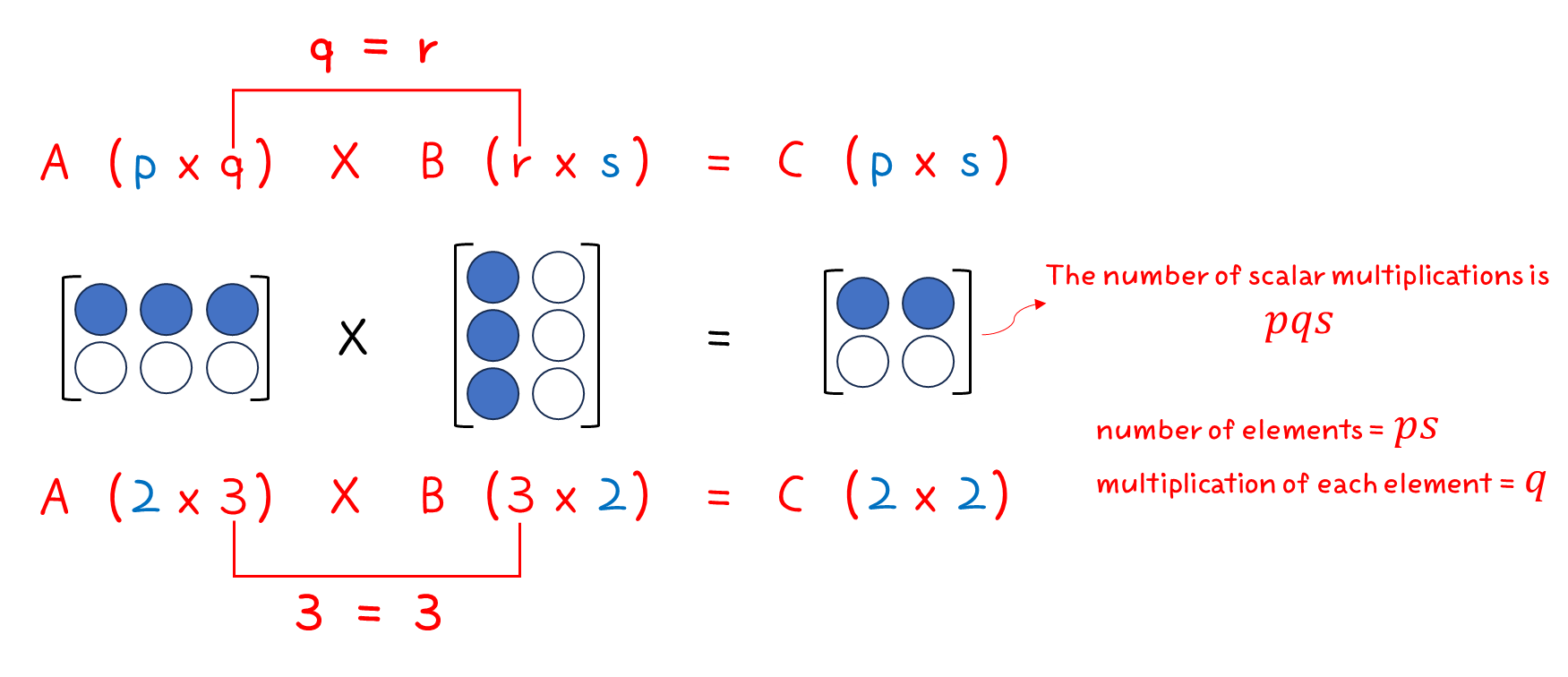
'행렬 곱'을 하기 위해서는 앞 행렬의 column 길이와 뒤 행렬의 row 길이가 같아야 한다.
그러면, 앞 행렬의 row 와 뒤 행렬의 column 길이만큼의 결과가 나온다.
두번째로 알아야할 내용은 행렬 곱에서 '결합 법칙'이 성립한다는 것이다.

그런데, 여기에서 우리가 주의깊게 살펴봐야할 사실이 하나 등장한다.
행렬 곱에서 결합을 어떻게 하는지에 따라 계산 횟수가 달라진다는 것이다.

위의 예시와 같이 3개의 행렬이 주어졌을 때,
계산 횟수를 살펴보면 10배의 차이가 발생한다는 것을 알 수 있다.
[Problem]
그러면 우리가 여기에서 해결하고자 하는 문제가 무엇일까?

곱셈을 해야하는 여러 행렬이 순서대로 주어졌을 때,
어떻게 결합을 해야 전체 계산 횟수를 최소화 할 수 있을지를 찾아내는 것이다.
[Brute force approach]
일단 무식하게 살펴보자.

총 4개의 행렬이 주어졌을 때, 총 5가지의 묶음 방법이 존재한다.
이를 분류해보면
앞에서부터 1개 묶음을 하면 총 2종의 결합 방법이 존재하고
2개 묶음을 하면 1종,
3개 묶음을 하면 2종의 결합 방법이 있기에 총 5종의 결합 방법이 있게 된다.
이 과정을 공식으로 살펴보면 다음과 같다.

공식을 유도하고 분석하는 것은 생략하도록 하겠다.
그런데, 이를 Asymptotic 하게 생각해보면, 다음과 같다.

마찬가지로 계산식 유도 및 분석은 생략하고.... 결론적으로 엄청난 경우의 수가 나오기에...
이렇게 문제를 푸는 것은 말이 안됨! ^^
[Solution]
똑똑하게 문제를 풀어보자.

지금까지 살펴본 내용을 공식화한 것으로 생각하면 된다.
위 공식을 가지고 직접 손으로 계산을 해보자.
행렬에 따라서 row와 column은 다음과 같이 살펴볼 수 있다.

왜 이렇게 표현이 되는지 이해가 안되면 안된다.
앞에서 충분히 살펴본 내용을 곰곰히 생각해보면 된다.
예시를 하나 들어보자.
행렬이 6개가 주어졌다고 했을 때, p값이 다음과 같이 제시 되었다고 해보자.
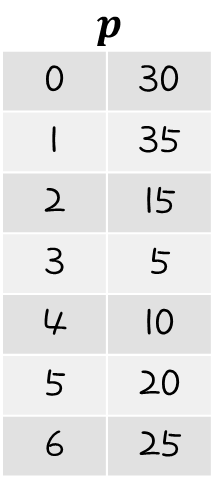
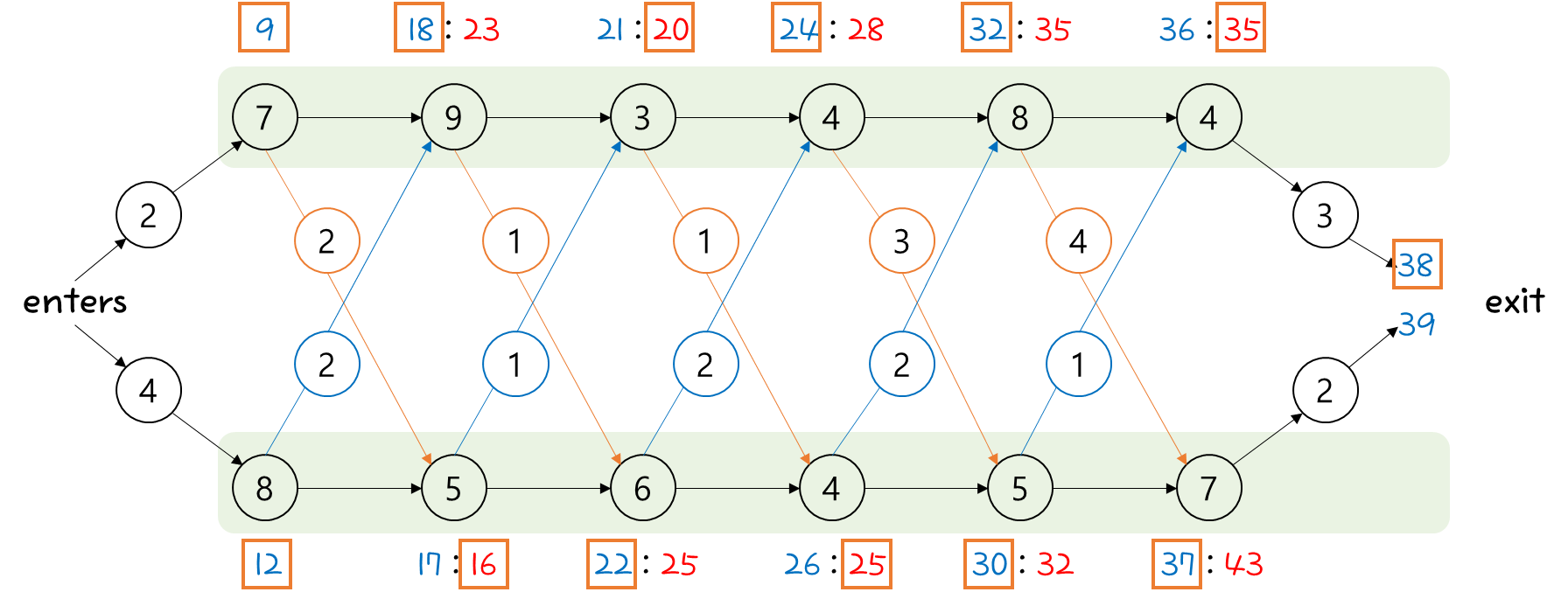
이 문제를 풀기 위해 우리는 m, s 행렬을 작성해야 한다.

왜 이렇게 하는지는 문제를 풀어보면서 알아보자.

위 공식을 살펴보면 알겠지만,
i=j 조건에서는 모두 0 값을 갖게 되고 i보다 j는 항상 커야 되기 때문에 표의 아랫부분은 계산하지 않아도 된다.
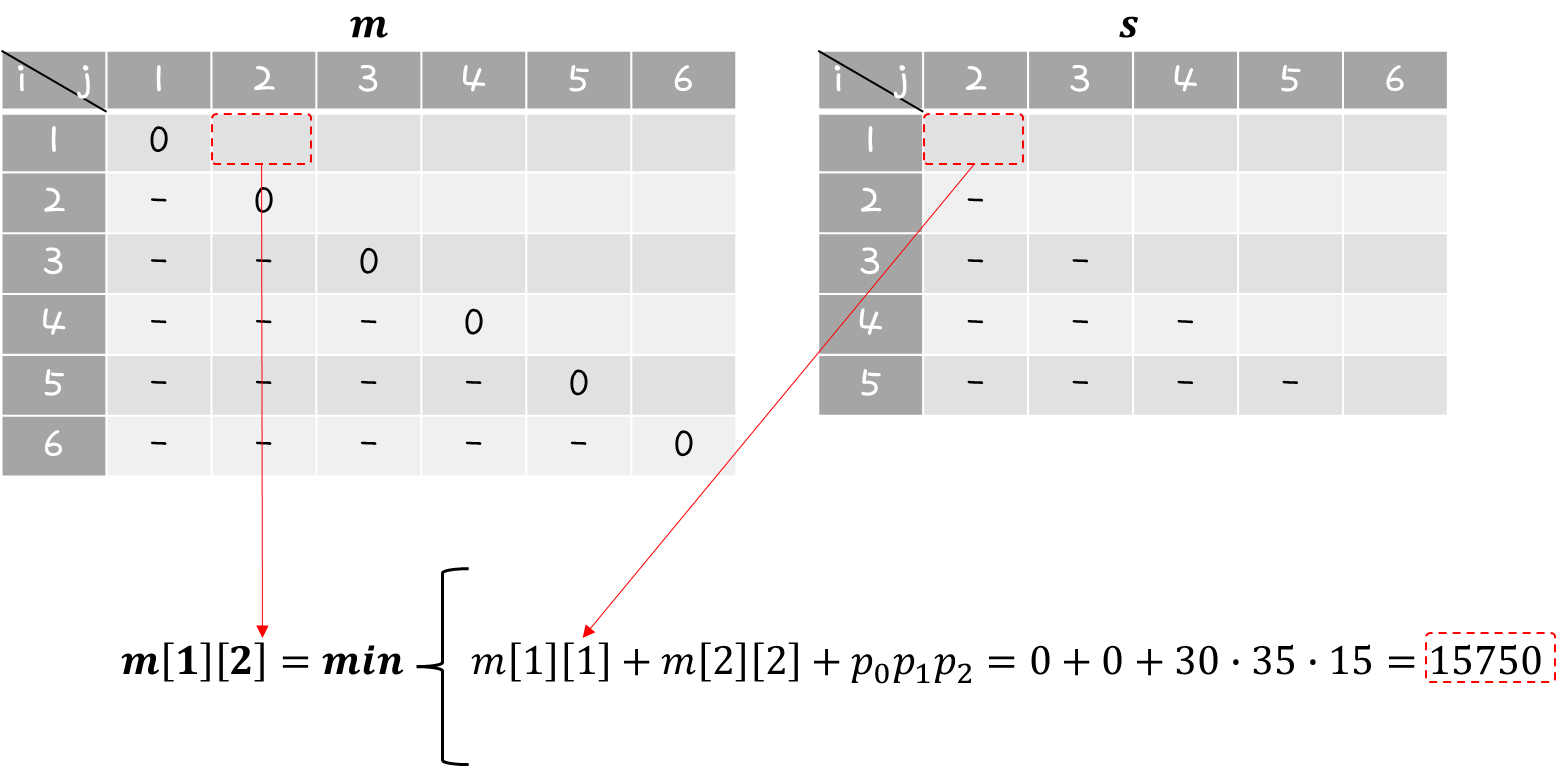
m[1][2] 값부터 계산해보면 위와 같이 정리해볼 수 있다.
k값은 ( i ≤ k < j ) 조건이므로 ( 1 ≤ k < 2 )와 같고, 그렇기 때문에 k값은 1밖에 갖을 수 없다.
s 행렬의 s[1][2] 값은 k값이 1이므로 1값을 작성하면 된다.
이런식으로 m[2][3], m[3][4], m[4][5], m[5][6] 부분을 채울 수 있다.

이번에는 m[1][3]을 계산해보자.
앞에서와 달리 k값은 ( 1 ≤ k < 3 )이므로, k값은 1, 2 의 2가지 경우가 있을 수 있다.
그러므로, 최종 결과가 2개 나오고, 그 중에서 min 값을 선택하면 된다.
k값이 1인 경우를 선택했으므로 s[1][3] 위치에는 1을 작성하면 된다.
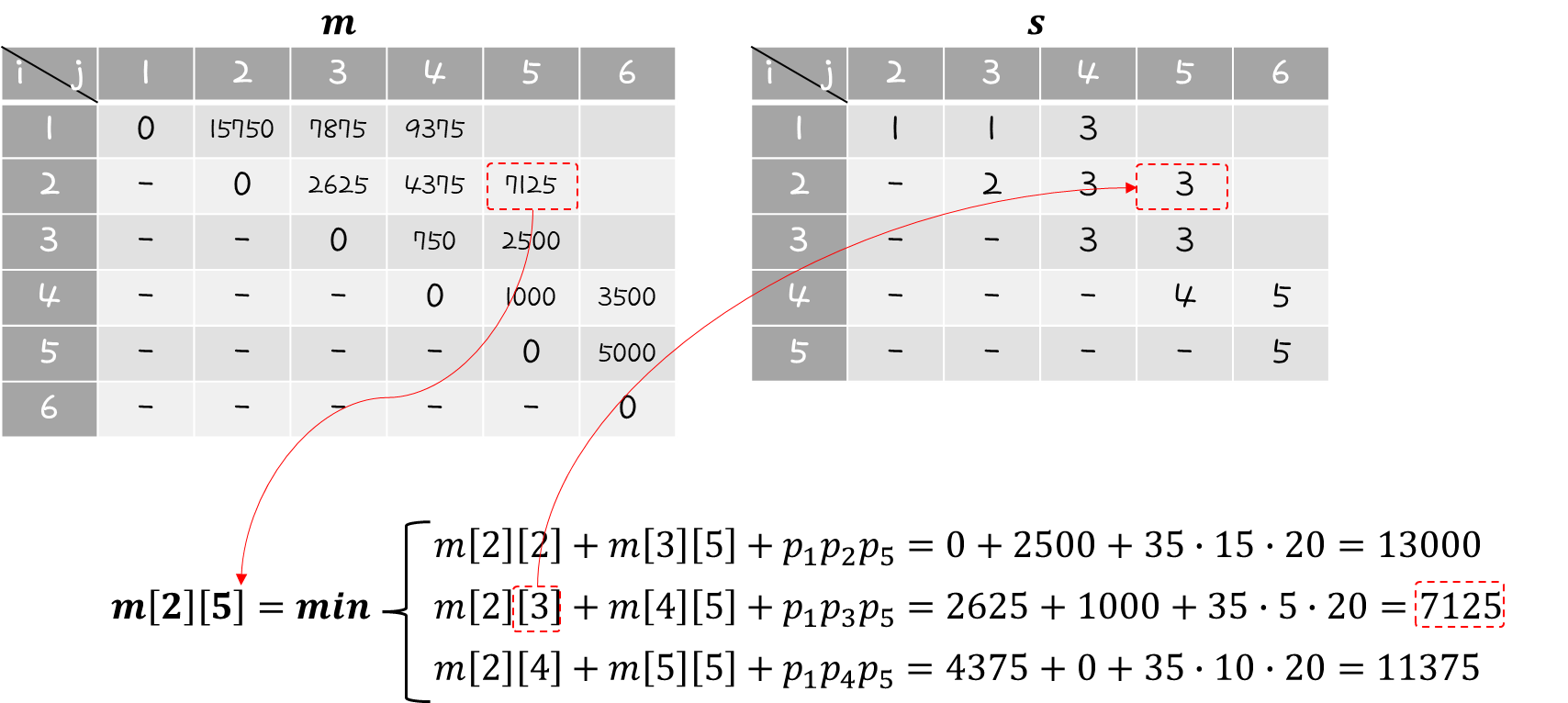
하나씩 하나씩 이렇게 채워나가면 된다.
전부 채우면 다음과 같다.
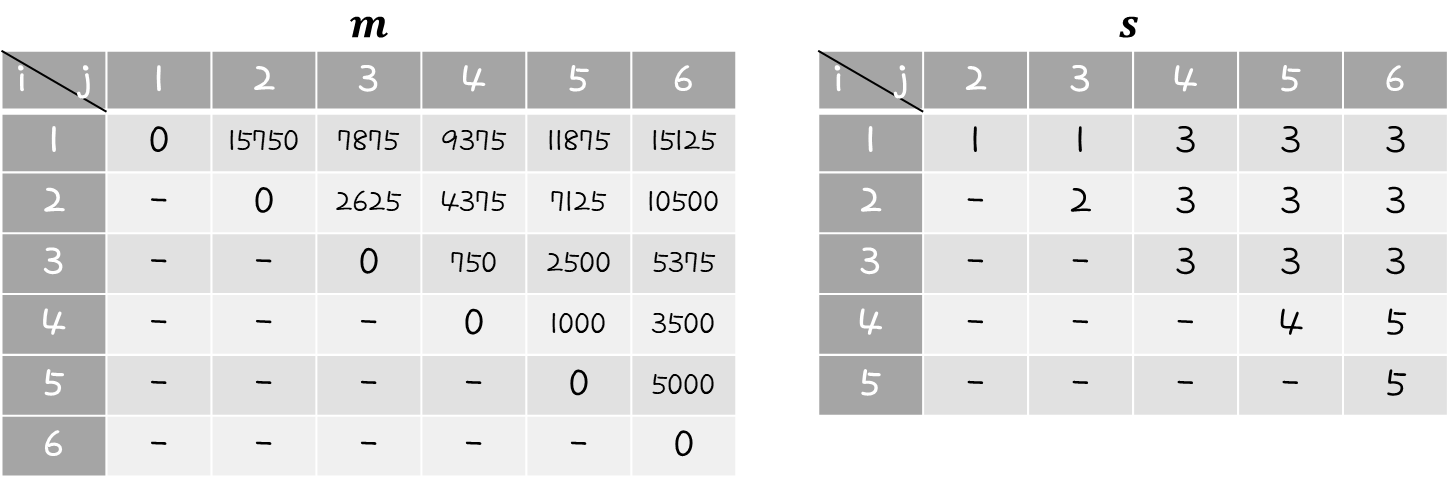
끝~
[Pseudo Code]
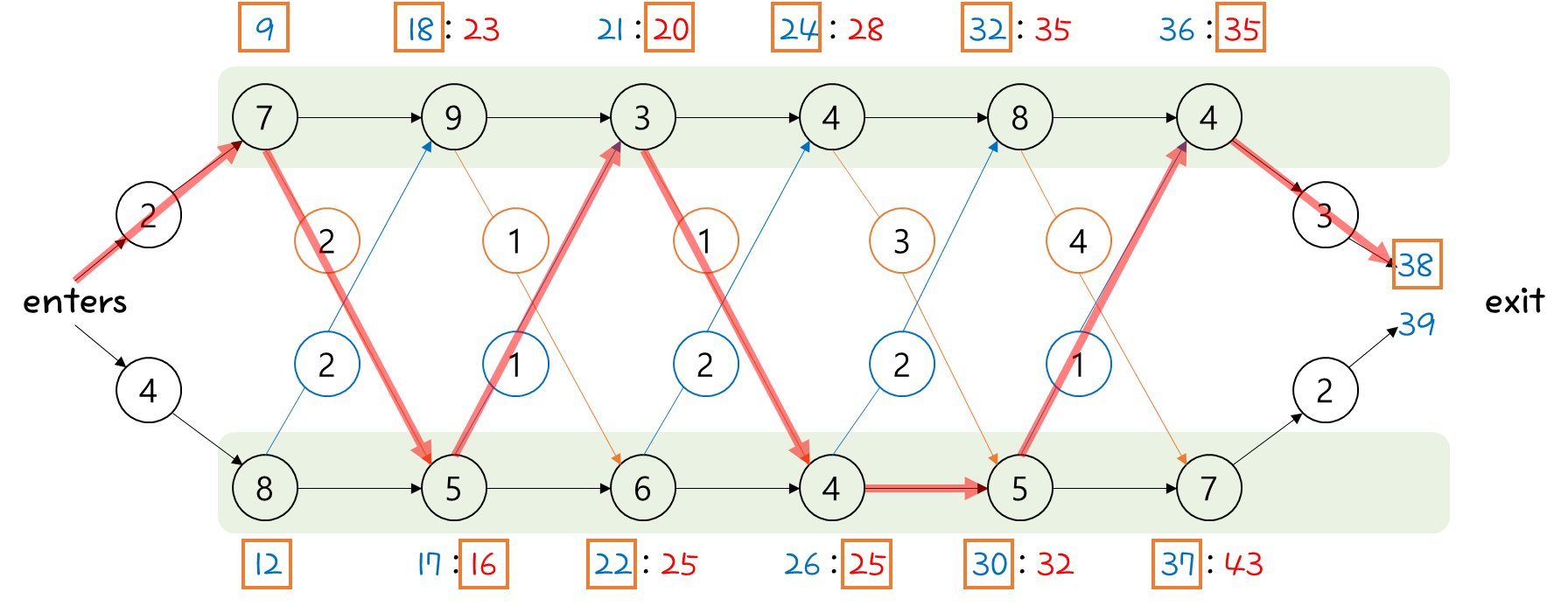
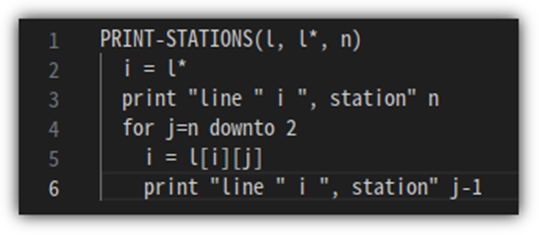
이 과정을 가지고 pseudo code로 만들어보자.
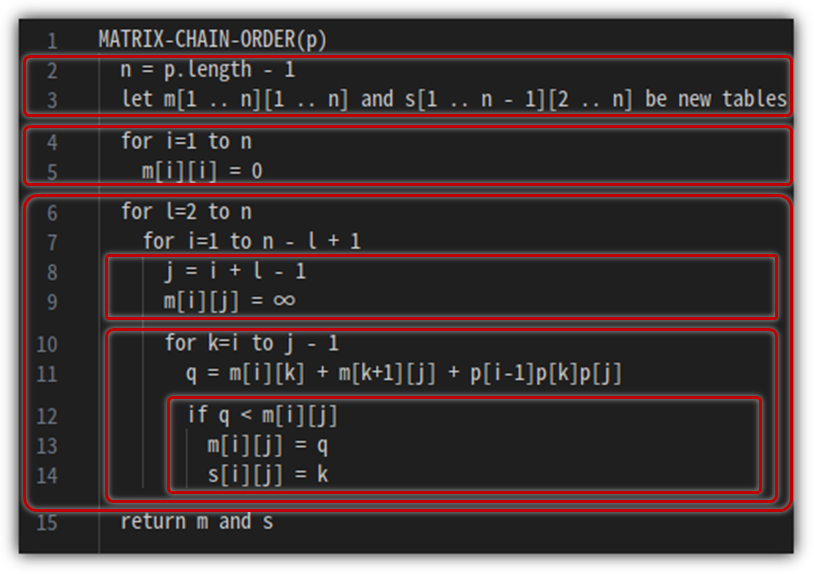
이렇게 만들어진 결과물을 출력하기 위한 code는 다음과 같다.
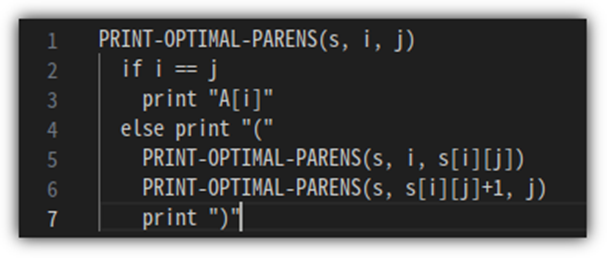
[Time & Space]
time complexity 와 memory space를 계산해보면 다음과 같다.
먼저 Time Complexity를 살펴보자.

무려 n의 3승 이다.
메모리 공간을 계산해보면 다음과 같다.

알고리즘을 위해 추가로 사용하는 메모리는 m, s 배열이 필요하다.
Asymptotic 하게 해보면.... 결국은 n의 제곱만큼의 공간을 필요로 한다.
'Programming > Algorithm' 카테고리의 다른 글
| 알고리즘 #3 - Greedy Algorithm #1 - An activity-selection problem #1 (0) | 2024.04.10 |
|---|---|
| 알고리즘 #2 - Dynamic Programming #3 - Longest-Common-Subsequence #1 (0) | 2024.03.25 |
| 알고리즘 #2 - Dynamic Programming #2 - Rod-Cutting #1 (0) | 2024.03.09 |
| 알고리즘 #2 - Dynamic Programming #1 - Assembly-line scheduling #1 (0) | 2024.02.28 |
| 알고리즘 #1 - 정렬 문제 #8 - Radix Sort #1 (1) | 2024.02.21 |