
[ Terminology & Problem ]
이번에 살펴보고자 하는 알고리즘은 "Longest Common Subsequence (LCS)" 이다.
어떤 문제를 해결하고자 하는 것인지 설명하기 전에 용어에 대한 정의부터 살펴보겠다.
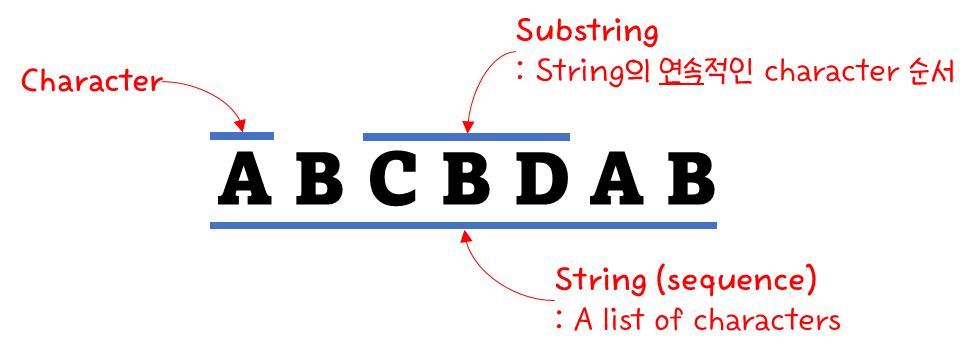
여기에서 주의깊게 살펴봐야 할 것은 "Substring"인데, 연속적인 character를 의미한다.
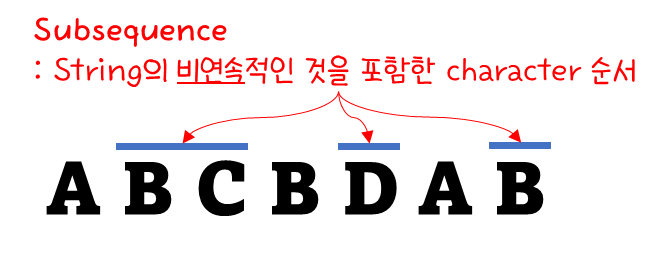
반면, "Subsequence"는 비연속적인 character 순서를 포함한다.

2개의 string이 주어졌을 때, 공통적으로 있는 subsequence를 "Common Subsequence"라고 한다.
그리고 "Common Subsequence" 중에서 가장 긴 길이를 갖는 것을 "Longest Common Subsequence (LCS)"라고 한다.
이런 LCS를 구하는 방법을 찾는 것이 이번 목표이다 ^^
[Brute force approach]
착실하게 (무식하게?) 찾는 방법은 다음과 같다.

당연히 이렇게 찾는 것은 말이 안된다.
입력 string의 갯수가 n개라고 했을 때 2의 n승만큼 subsequence가 나오기 때문이다.

[Notation]
이후 설명할 내용에서 사용하는 notation을 정리하면 다음과 같다.
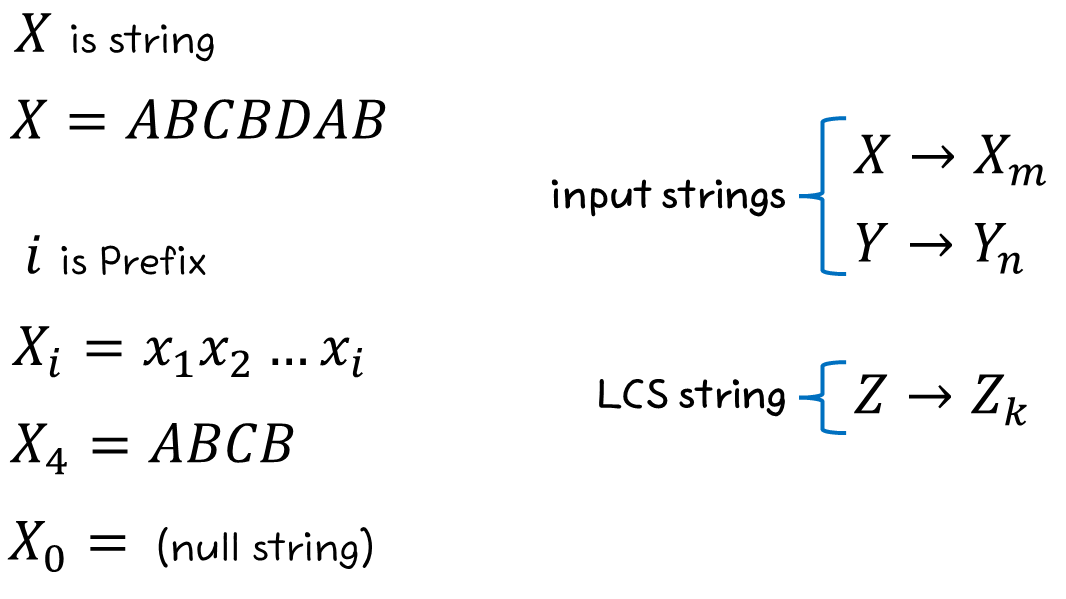
[Idea]
똑똑하게 해결하기 위한 아이디어는 다음과 같다.

복잡해보이는데, 가만히 살펴보면 엄청 당연한 이야기를 하고 있다.
특정 위치의 chracter가 같다면 LCS는 그 같은 값은 일단 LCS에 포함되는 것이고,
각 입력 string에서 동일한 값보다 1씩 작은 string의 LCS값을 더해주면 전체 LCS가 된다.
반면, 특정 위치의 chracter가 같지 않다면 LCS는 입력 string중 하나의 값을 1 차감한 내역으로 다시 LCS를 구하면 된다.
[ Longest Common Subsequece - Dynamic Programming Algorithm ]
위의 아이디어를 정리하면 다음과 같은 알고리즘이 된다.

이걸 어떻게 하는 것인지 살펴보자.
다음과 같은 2개의 string이 입력되었을 때 다음과 같은 표를 그리고 초기화 하자.
- X = ABCBDAB
- Y = BDCABA

앞에서 정리한 알고리즘을 기반으로 하나씩 값을 채워나가면 된다.

① x ≠ y 이므로 둘 중 큰 값 선택해야 하는데, 둘 모두 0이므로, 0
② ③ 상동
④ ⑥ x = y 이므로, 왼쪽 대각선 위의 값 + 1
⑤ x ≠ y 이므로 둘 중 큰 값 선택해야 하는데, ④ 값이 1이므로, 1
그리고, 어느 곳에서 값을 받아갔는지 화살표로 표기 해줘야 한다.
이런식으로 하나씩 값을 작성해 나가면 다음과 같이 된다.

LCS값이 어떻게 되었는지는 다음과 같이 추적해볼 수 있다.

화살표를 보면 알겠지만, 정답이 하나만 있는 것은 아니다.

[Pseudo Code]
손으로 진행했던 것을 코드로 만들어 보자.
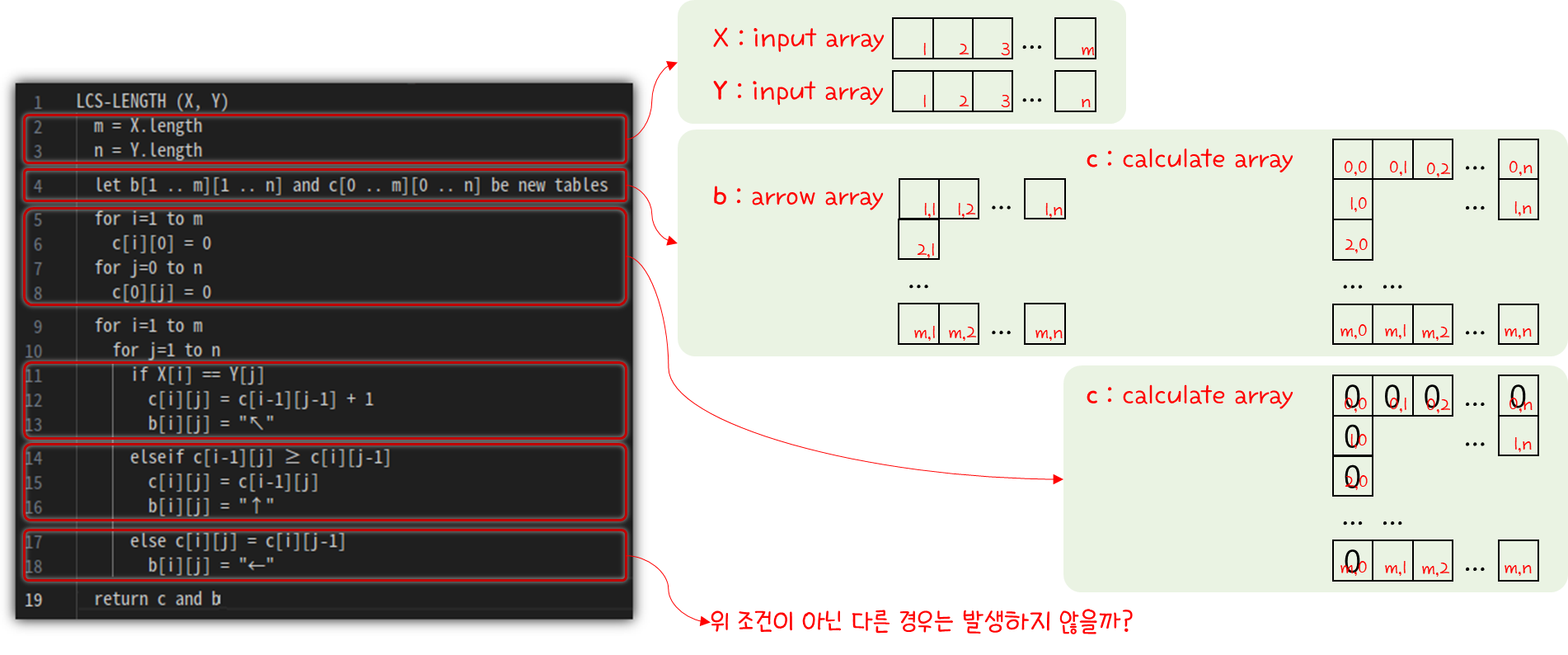
손으로 진행했던 것과 차이가 있는 부분 위주로만 설명해봤다.
위 표에서 화살표를 살짝 끄적였는데, code에서는 b array를 통해 기록하도록 했다.
결과를 출력하기 위한 코드는 다음과 같다.

[Time & Space]
code를 보면 직관적으로 파악 가능한 것 처럼 Time complexity는 다음과 같다.

Space는 b array + c array 공간이 추가적으로 필요하기에 다음과 같다.
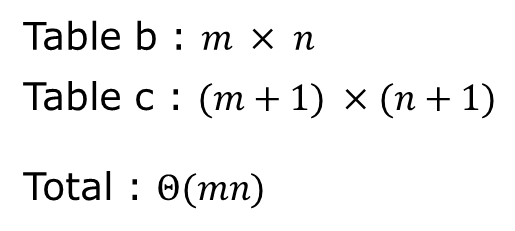
그런데, Space를 줄일 수 있는 경우가 있다.
실제 String 정보까지는 필요없고, 길이값만 필요하다고 하면 다음과 같이 작은 space만 필요로 한다.

또 다른 경우로는 다음과 같은 case가 있을 수 있다.

LCS에 대해서는 여기까지~
'Programming > Algorithm' 카테고리의 다른 글
| 알고리즘 #3 - Greedy Algorithm #1 - An activity-selection problem #1 (0) | 2024.04.10 |
|---|---|
| 알고리즘 #2 - Dynamic Programming #4 - Matrix-Chain Multiplication #1 (0) | 2024.04.07 |
| 알고리즘 #2 - Dynamic Programming #2 - Rod-Cutting #1 (0) | 2024.03.09 |
| 알고리즘 #2 - Dynamic Programming #1 - Assembly-line scheduling #1 (0) | 2024.02.28 |
| 알고리즘 #1 - 정렬 문제 #8 - Radix Sort #1 (1) | 2024.02.21 |