
기사 작위를 갖고 계시는 '토니 호어'로 불리우시는 분이 1961년에 발표한 정말 정말 유명한 알고리즘이다.
이름 그대로 제일 빠른 정렬 알고리즘이 뭐야? 라고 하면 누구나 외치는 "퀵 정렬" !!!
(참고로 '토니 호어'님은 아직도 시니어 연구원으로 계신다고 한다. 무려 90세의 나이임에도 .... @.@)
[ 공부 목차 ]
① Partition
② Balanced partitioning vs Unbalanced partitioning
③ Randomized-Partition
④ Quick-Sort
① Partition (vanilla Partition)
- 'Quick Sort'에 있어서 가장 중요한 개념이 바로 partition 이다.
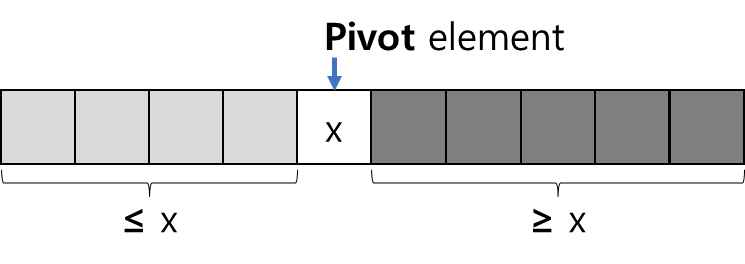
- 기준값(Pivot element) 보다 작은 값은 왼쪽에, 큰 값은 오른쪽에 배치하여 나누는 것을 의미한다.
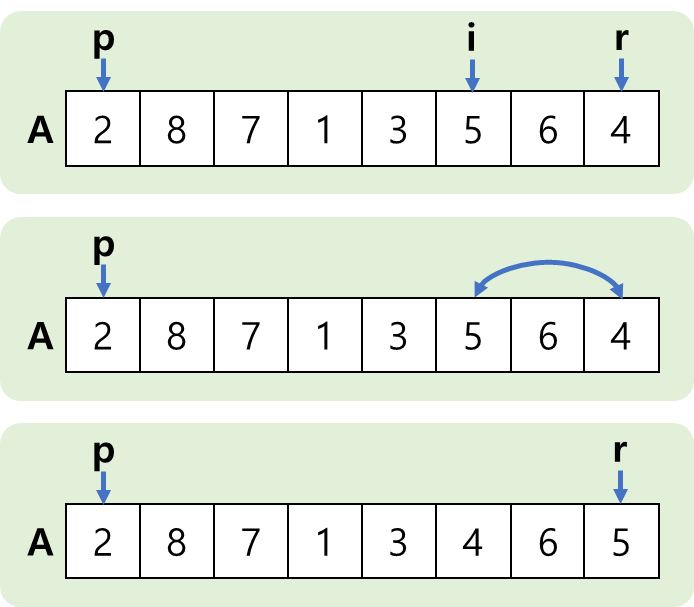
- 가장 기본이 되는 partition 방법은 제일 오른쪽 값을 pivot으로 해서 하나씩 비교하는 것이다.
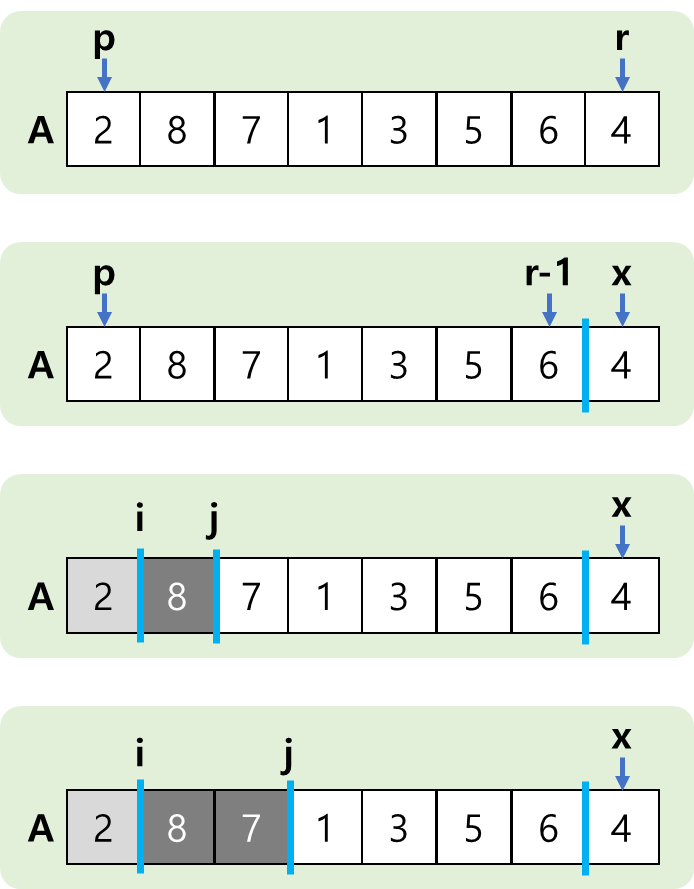
- 제일 오른쪽 값을 기준으로 제일 왼쪽부터 하나씩 비교해서 작은값 그룹과 큰값 그룹을 만들어 간다.
- 그런데, "1"값을 만났을 때 작은값 그룹에 묶을 때가 문제가 된다.

- 이럴 때에는 큰값의 제일 왼쪽에 위치한 것과 swap을 하면 된다. (i값 위치의 변화도 살펴봐야 한다)
- 이렇게 하다보면 끝까지 진행을 하게 될텐데, 마지막에 위치한 pivot 값은 어떻게 해야할까?
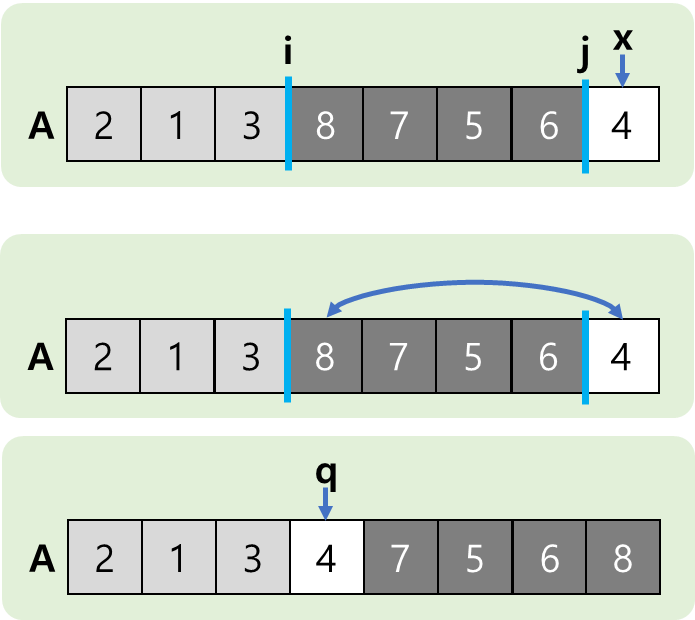
- 역시 마찬가지로 큰값의 제일 왼쪽값과 swap 하면 된다.
- 이 과정을 pseudo code로 살펴보면 다음과 같다.
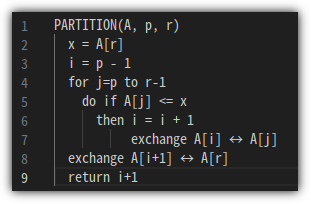
- Running Time을 계산해보면 다음과 같다.


② Balanced partitioning vs Unbalanced partitioning
- partitioning을 할 때에 좌우 균형이 잘 맞춰져서 나뉘어지면 좋겠지만,
- 그렇지 않고 한 쪽에 치우칠 수도 있다.
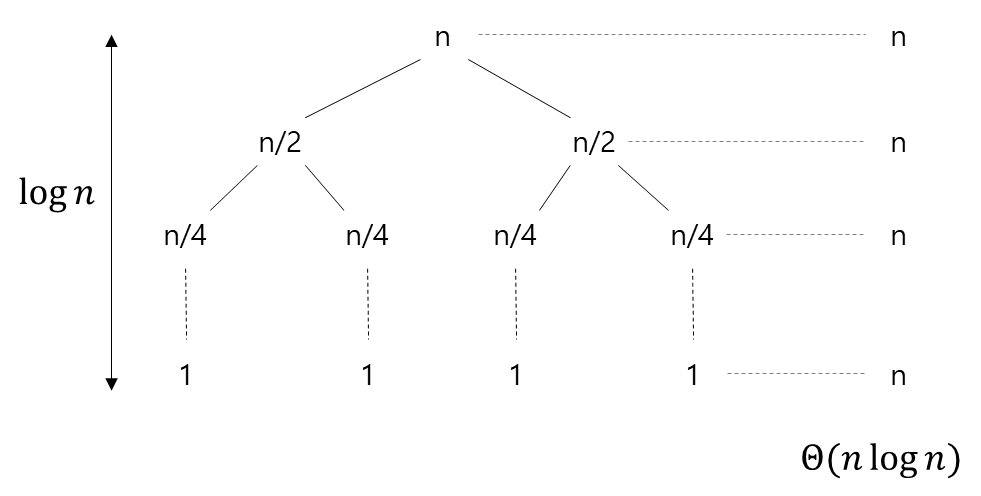
- 균형이 맞지 않는 극단적인 경우를 보면 다음과 같다.

- Running Time은 다음과 같이 구할 수 있다.

- 즉, 최악의 상황에서는 n제곱, 보통은 n로그n 이라고 정리하면 되겠다.
- 그러면, 최악의 상황을 막을 방법은 없을까!?
③ Randomized-Partition
- 최악의 상황이 발생하는 것은 pivot 값을 무조건 제일 끝값을 택하기 때문에 발생을 한다.
- 그러면, pivot 값을 random하게 선택을 하게 되면 최악의 상황이 벌어질 가능성을 낮출 수 있다.

- random하게 값을 뽑아서, 그것을 제일 오른쪽(끝) 값과 swap을 한 다음에 partition을 하면 되는 것이다.
- 그런데, radom 호출 하는 것 자체가 over-head가 될 수도 있다. radom 자체가 비용이 크기 때문이다.
- 그래서, (첫값 + 가운데값 + 끝값) 3개 중에 중간값을 선택하는 방법도 있긴 하다.
④ Quick-Sort
- 지금까지 우리는 Partition을 공부했다. 이를 이용해서 Sort는 어떻게 할 수 있을까!?
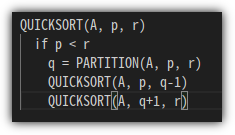
- 일단 partition을 한 다음, 왼쪽/오른쪽 각각 QuickSort를 하면 된다.
- 그렇다 !!! Divide-and-Conquer 알고리즘이다.

- Quick-Sort의 Running Time은 어떻게 될까?
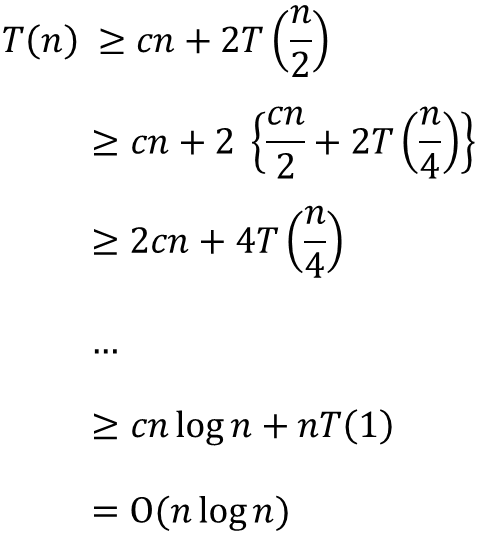
- 메모리 사용은?! 위치를 가르칠 변수 정도면 충분하다. 즉, 입력 데이터의 크기에 영향을 받지 않는다.
지금까지 여러 Sorting algorithm을 알아봤는데, 성능 비교 등을 해보면 좋을텐데...^^
다음 기회로~~~
'Programming > Algorithm' 카테고리의 다른 글
| 알고리즘 #1 - 정렬 문제 #7 - Counting Sort #1 (0) | 2024.02.21 |
|---|---|
| 알고리즘 #1 - 정렬 문제 #6 - Lower bounds #1 (0) | 2024.02.20 |
| 알고리즘 #1 - 정렬 문제 #4 - Heap Sort #1 (0) | 2024.01.20 |
| 알고리즘 #1 - 정렬 문제 #3 - Merge Sort #1 (0) | 2024.01.06 |
| 알고리즘 #1 - 정렬 문제 #2 - Growth of Functions (0) | 2023.12.25 |
