
"Radix"가 뭘까?
'기수(基數)'는 0~9까지 기본이 되는 수를 의미하는데, 여기에서는 '진법(進法)'의 의미가 더 큰 것 같다.

"Radix Sort"의 다른 호칭은 다음과 같다.
- 기수 정렬
- Bucket Sort
- Digital Sort
Radix Sort 알고리즘도 역사가 오래된 아이인데, 1923년에 이미 천공카드 분류 방법으로 널리 사용되었단다.
(어!? 천공카드가 뭔지 아는 것 만으로도 년식 인증인가!?)
① MSD (Most Significant Digit, 최상위 유효숫자)
- 앞(큰) 자리 부터 정렬을 해 나가는 방식이다.
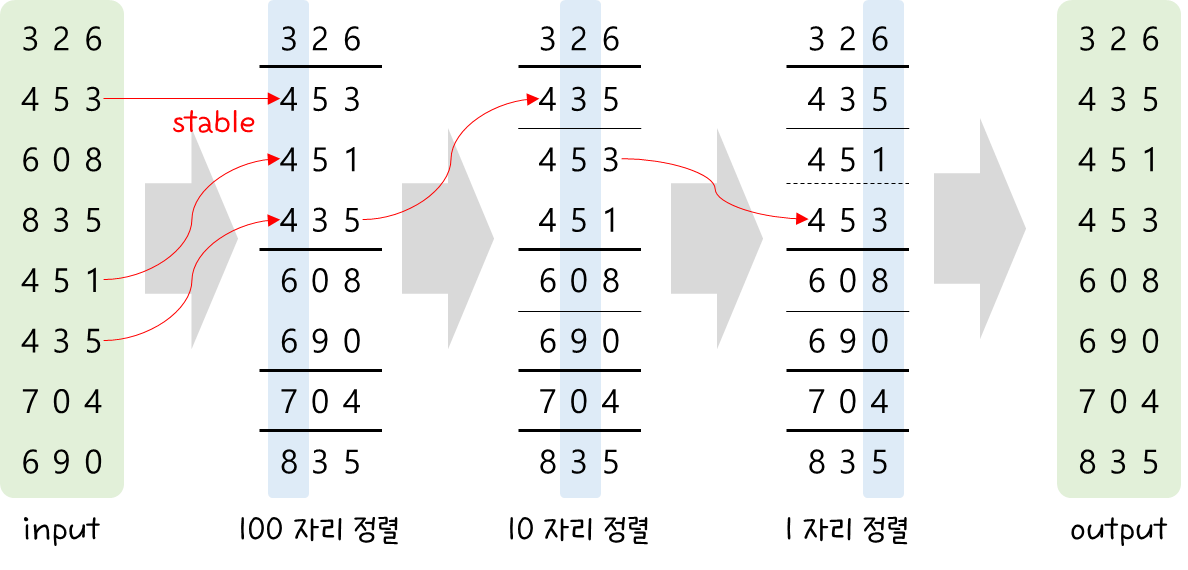
- 중간에 가로로 있는 구분선 위치 정보는 중요하다.
- 단계 별로 구분선 안에서만 정렬이 이루어져야 하기 때문이다.
② LSD (Least Significant Digit, 최하위 유효숫자)
- MSD 방식과 정반대로 뒤(작은) 자리 부터 정렬을 해보자.

- Stable 이라는 속성을 정말 잘 이용한 방법으로 보인다.
- MSD와 다르게 가로줄(각 단계에서의 구분 위치) 정보를 관리할 필요가 없다.
- 아랫 자리들이 이미 sorting이 되어있기 때문에 윗 자리 sorting을 하면 전체가 sorting 된다.
③ Pseudo Code
- 너무 추상적일 수 있지만, 일단 다음과 같이 Pseudo Code를 정리할 수 있다.
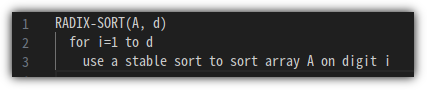
- 여기에서 중요한 것은 "stable sort" 방식이어야 한다는 점이다.
④ Running Time
- 우리는 바로 전에 훌륭한 stable sort 알고리즘 중 하나를 공부했었다 → Counting Sort !!!
- Counting Sort 알고리즘을 이용해서 Radix Sort를 해본다고 가정하면, 다음과 같다.

- 위 내용을 정리하자면, 다음과 같다.
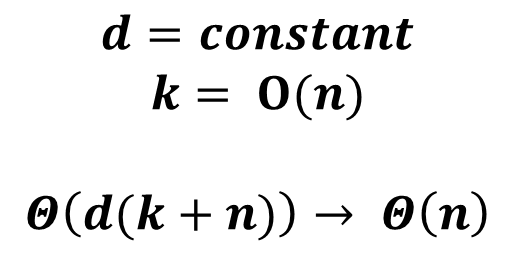
⑤ Changing d and k
- 우리가 지금까지 다루는 방식은 다음과 같다.
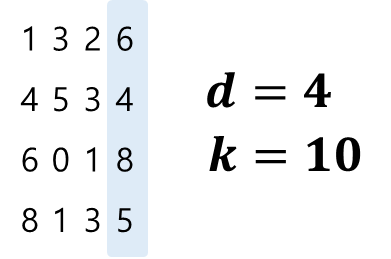
- 하지만, 이것을 좀 다르게 처리할 수도 있다.
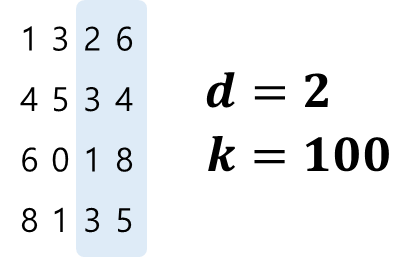
- 응?! 10진법이 아니라 100진법(진수)으로 처리할 수도 있다는 것이다.
⑥ optimal r
- 일단 아래 그림을 잘 살펴보고 각 변수값의 정의를 확인하자.
- n개의 b-bit 숫자가 있다고 했을 때, r 묶음으로 처리를 하는 경우이다.
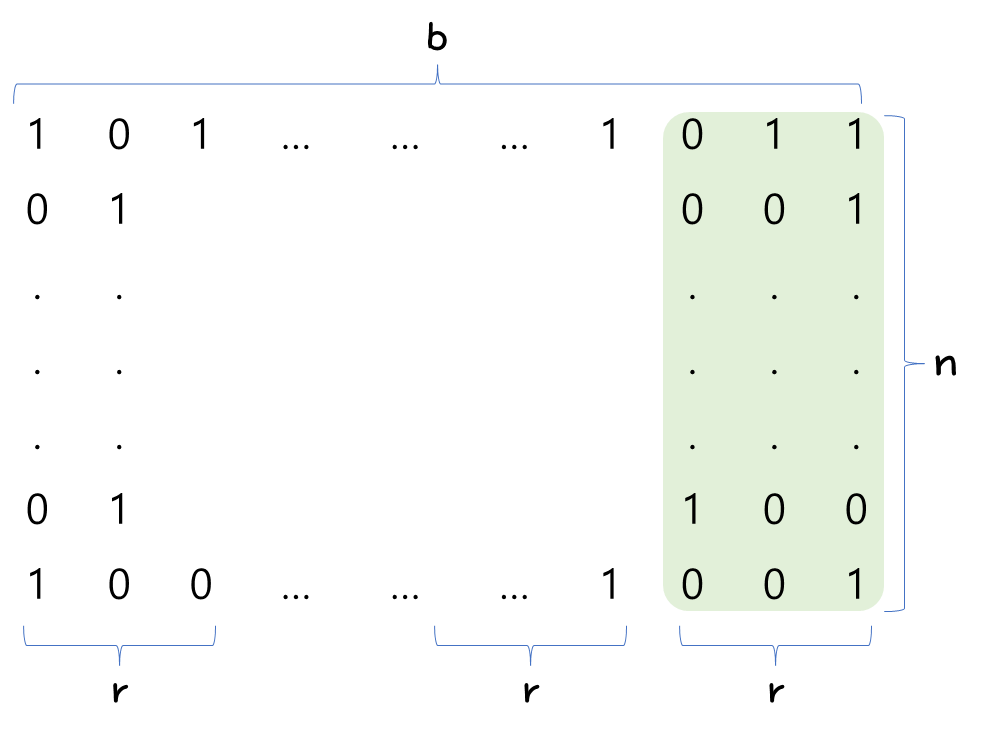
- 이럴 때, 우리는 다음의 최적해 r 값을 찾아야 하는 것이다.

- 2 가지 경우로 나누어서 생각해보자.

- 위의 경우는 입력값 개수에 비해서 b값이 많이 작을 경우이다.
. 이 때는 굳이 나누지 말고 통으로 (하나로) 묶어서 정렬을 해도 충분하다는 의미이다.
- 다른 경우는 다음과 같다.
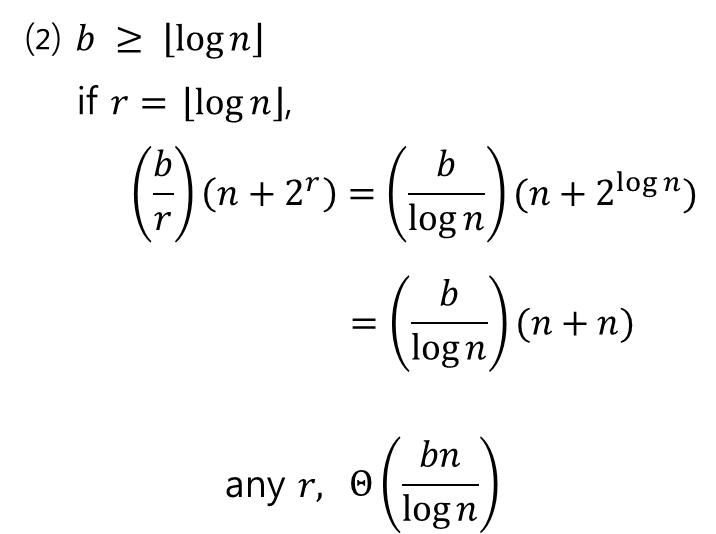
- 입력값 개수보다 값 자체가 길면, 좀 나누어서(log n 정도) 정렬을 하는 것이 좋다는 의미이다.
⑦ extra memory
- 앞에서 살펴봤겠지만, 일단 Radix Sort는 in place 알고리즘은 아니다.
⑧ memory copy
- d 값만큼 정렬 step이 발생하는데, 이 때마다 값들을 복사해야하는데 이로 인한 cost가 크다.
뭔가 좀 어수선하게 설명이 되었는데,
전체적인 흐름은 파악이 되었을거라 기대해본다.
'Programming > Algorithm' 카테고리의 다른 글
| 알고리즘 #2 - Dynamic Programming #2 - Rod-Cutting #1 (0) | 2024.03.09 |
|---|---|
| 알고리즘 #2 - Dynamic Programming #1 - Assembly-line scheduling #1 (0) | 2024.02.28 |
| 알고리즘 #1 - 정렬 문제 #7 - Counting Sort #1 (0) | 2024.02.21 |
| 알고리즘 #1 - 정렬 문제 #6 - Lower bounds #1 (0) | 2024.02.20 |
| 알고리즘 #1 - 정렬 문제 #5 - Quick Sort #1 (0) | 2024.02.06 |
