알고리즘 #1 - 정렬 문제 #1 - Insertion Sort #2

알고리즘을 구현하기 위한 소스 코드의 소요 시간(실행에 필요한 시간)은 어떻게 측정할 수 있을까?

 

출처: chatgpt

 

 

실행을 시켜서 완료될 때 까지 걸린 시간을 측정하면 될까?

 

실행하는 컴퓨터의 CPU가 무엇인지, HDD 또는 SSD를 사용하는 지와 같은 여러 상황에 따라서

똑같은 알고리즘도 시간이 다르게 나올 수 있을텐데...

 

그리고 작성하는 프로그래밍 언어에 따라서도 실행 시간은 천차만별일 수 있다.

 

즉, 실제 시간을 측정해서 알고리즘의 성능을 비교 평가하는 것은 어렵다.

 

 

그래서, 보통은 Pseudo code의 라인별 수행하는 횟수를 카운트 하는 방식으로 소요 시간을 측정한다.

 

 

Insertion sort의 pseudo code는 다음과 같다.

 

insertion pseudo code

 

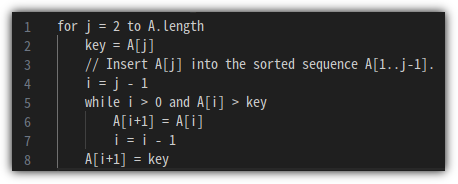
한 줄씩 살펴보자.

 

line #1

 

입력값 A의 길이가 n이라고 해보자.

보통의 프로그래밍 언어에서 배열은 0부터 시작하지만 pseudo code에서는 1부터 시작한다.

그러면 1번 라인은 총 몇 번 수행이 될까?!

 

지금 대답을 하지 못하는 분은 개발자로서 조금 문제가 있는 상태이고 (^^)

"n - 1"번이라고 대답하신 분은 보통의 개발자 수준이고

"n"번이라고 대답하신 분은 정말 훌륭한 개발자 이거나 아니면 운으로 맞춘 분일 것이다 ^^

 

"j = 2"라고 되어 있기에 for문 자체는 "n - 1"번 수행한다고 말하는 것이 일반적이지만

실제 for문 자체는 마지막 조건 체크를 위해 한 번 더 수행을 하기 때문에 "n - 1 + 1"번 수행을 하게 된다.

하지만, 그냥 "n - 1"번 수행한다고 해도 무방하지 싶다.

 

line #2 ~ #4

 

2번 ~ 4번 라인은 각각 "n - 1"번 수행한다.

 

line #5 ~ #7

 

5번 ~ 7번 라인이 핵심인데...

처음 "j = 2" 상황에서는 1번 위치에 있는 값하고만 비교하면 되기에 1번만 실행이 될 것이고,

그다음 "j = 3" 상황에서는 2번 위치하고 비교하고 그 다음 1번 위치하고 비교를 하게 된다.

그렇게 해서 "j = A.length" 상황에 되면, 즉 "j = n" 상황이 되면 "n - 1"번 비교를 하게 된다.

이걸 그림으로 표현해보면 아래와 같다.

 

while문 상황

 

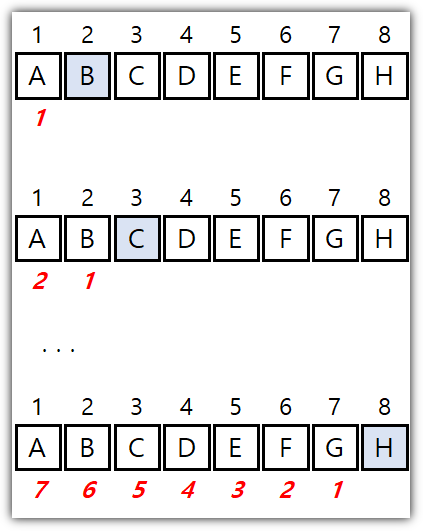
그래서, while문이 있는 5번 라인은 "1 + 2 + 3 + ... + n"번 실행을 하게 되고 (값 비교를 위해 한 번 더)

6번, 7번 라인은 "1 + 2 + 3 + ... + (n -1)"번 실행을 하게 된다.

 

line #8

 

8번 라인은 당연히 "n - 1"번 수행한다.

 

 

잘 이해가 되시나요?!

여기에서 "예"라고 대답을 하신 분은 .... No! No!! No!!!

 

중간에서 끝

 

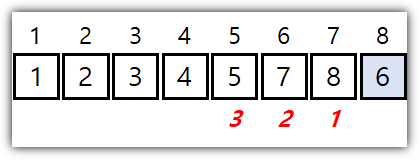
8번째 값을 정렬할 차례가 와서

첫번째로 7번 위치랑 비교 =  pass, 6번 위치 비교 = pass

5번 위치랑 비교했더니 여기에서 break

 

8번째 값을 정렬할 때에는 7번의 비교가 필요한 줄 알았는데,

실제 입력값 상황에 따라 수행 횟수가 가변적이다.

 

그래서 이를 t변수를 이용해서 표현한다고 하면, 전체적으로 다음과 같이 정리해볼 수 있다.

 

running time

 

C 변수는 각 라인을 실행할 때 드는 비용(시간)을 의미한다.

그래서 위 내용을 정리해서 총 실행 시간은 다음과 같이 정리할 수 있다.

 

The sum of product of cost and times of each line

 

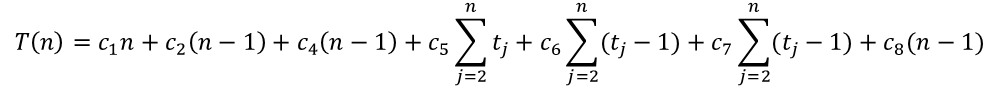
여기에서 뭔가 답답하게 만드는 것이 t 변수 값인데,

best/average/worst case에 따라서 값이 달라질 수가 있다.

 

best / worst cases

 

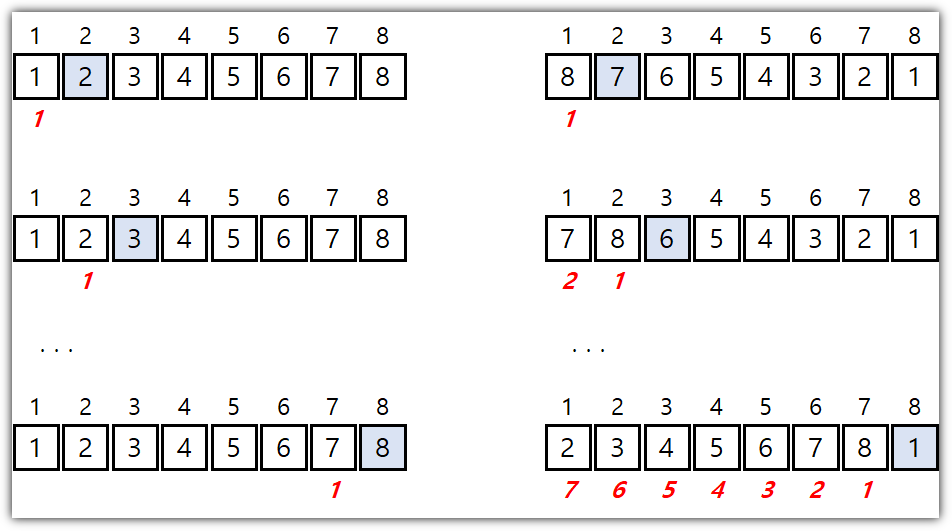
위 그림에서 왼쪽이 best case이고, 오른쪽은 worst case이다.

다시 말해 이미 정렬이 되어 있는 경우는 best case이고, 역으로 정렬된 경우가 worst case이다.

 

best case에 대해서 정리해보면 다음과 같다.

 

best case

 

결론적으로는 an + b 형식의 식으로 나오고 이는 선형적인 모습을 보인다.

 

이번에는 worst case를 살펴보자.

 

worst case

 

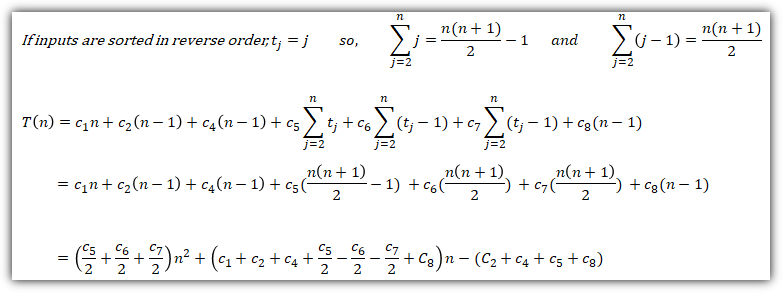
정리된 식을 살펴보면,

worst case는 an^2 + bn + c 와 같은 2차 함수 형태로 나타난다.

 

 

best case는 입력값 n의 크기가 커짐에 따라 선형적으로 실행 시간이 증가하게 되고

worst case는 입력값 n의 크기가 커짐에 따라 제곱으로 증가하게 된다는 것을 알 수 있다.

 

 

그런데, 모든 알고리즘들에 대해서 이렇게 분석하는 것은 너무 어렵다.

이와 같은 과정을 뭔가 단순하면서 명확하게 표현하는 것에 대해서 알아보도록 하자.

지금 말고 다음에.... ^^