함수의 증가? 함수의 성장? 함수의 성장률?
한글로 어떻게 표현해야 하는지 좀 애매한 타이틀인데,
구글링을 해봐도 명확하게 번역한 명칭이 확인되지 않는다.
보통은 그냥 "함수의 성장" 정도로 번역하면 적당한 것으로 보인다.
여기에서 하고 싶은 말이 무엇이냐면,
입력값에 대한 결과값, 즉 함수의 값이 어떻게 변화(증가/성장)하는지를 살펴봐야 한다는 것이다.
특히 우리는 지금 알고리즘 공부를 하기 때문에 이에 특화되어 정의해보자면,
입력 크기(n)에 따라 얼마나 많은 시간이나 공간을 필요로 하는 것인지를 살펴보는 것이다.
▶ Notation (표기법)
알고리즘의 성능, 즉 소요시간을 표현하는 3가지 notation을 먼저 알아보자.
① Θ-notation (Big-Theta) : tight
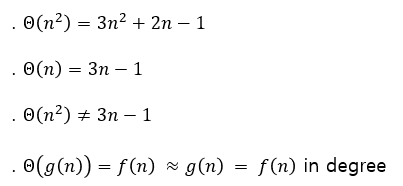
아주 정확하게 일치하는 것은 아니지만, 최대한 근접하게(tight) 표현하는 방법이다.
② Ο-notation (Big-O) : upper-bound
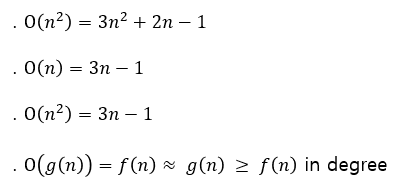
O-notation으로 표현한 값이 실제값과 같거나 더 큰 범위이기 때문에 upper-bound 라고 한다.
③ Ω-notation (Big-Omega) : lower-bound
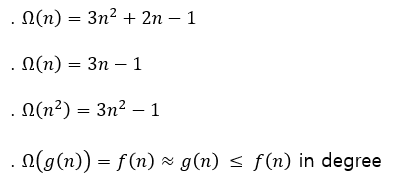
Ω-notation으로 표현한 값이 실제값과 같거나 더 작은 범위에 속하기 때문에 lower-bound 라고 한다.
보통 'Big-O'라고 부르는 O-notation만 알고 있는 사람도 많은데(me...??? ^^),
위와 같이 3가지 표기법이 존재하고 있고 주로 많이 사용하는 것이 Big-O notation이다.
▶ Asymptotic Notation (점근 표기법)
정확히 문장으로 설명하기에 쉽지 않지만 위와같은 표기법에서 보는 것처럼
정확히 일치하지는 않지만 어떤 추세/경향을 대강(?!) 보여줄 수 있는 표기법을 Asymptotic Notation이라고 한다.
▷ O-notation
- 아래 그래프를 잘 분석해야 한다. 상당히 많은 의미가 내포되어 있다.
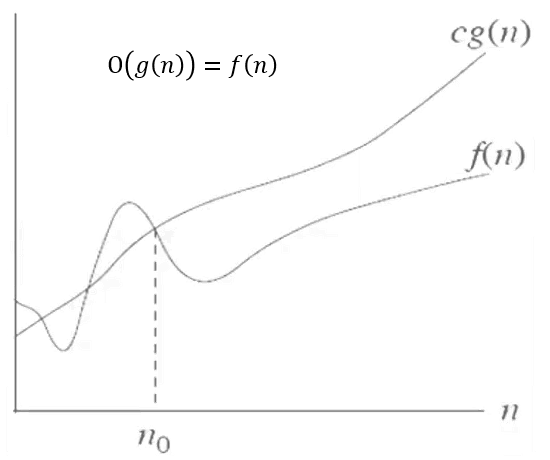
일단 g(n)과 f(n)만 놓고 앞 부분을 살펴보면
때로는 g(n)이 더 높은 값을 갖기도 하고 f(n)이 더 크기도 하다가
어느 순간, n0 값 이후로 g(n)이 지속적으로 더 큰 값을 갖는다.
g(n)도 잘 살펴보면 그냥 g(n)이 아니라 양의 상수 값 c 를 곱한 c * g(n) 값이다.
앞에서의 n0 값 역시 양의 값이다.
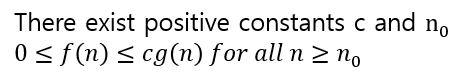
위와 같이 깔끔하게 요약할 수 있다.
이럴 때 g(n)은 f(n)의 asymptotic upper bound라고 부를 수 있다.
여기에서 문제를 한 번 풀어볼까!?
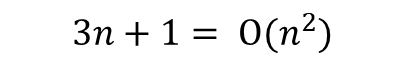
위 식이 성립함을 증명해보자.
막막할 수 있으니 바로 설명을 보자면 (^^) 다음과 같다.

여기에서 가장 중요한 부분은 첫 줄이다.

이 문장만 이해할 수 있으면 Asymptotic notation에 대해서 이해한 것이다.
▷ Ω-notation
- 마찬가지로 그래프를 하나 보자.
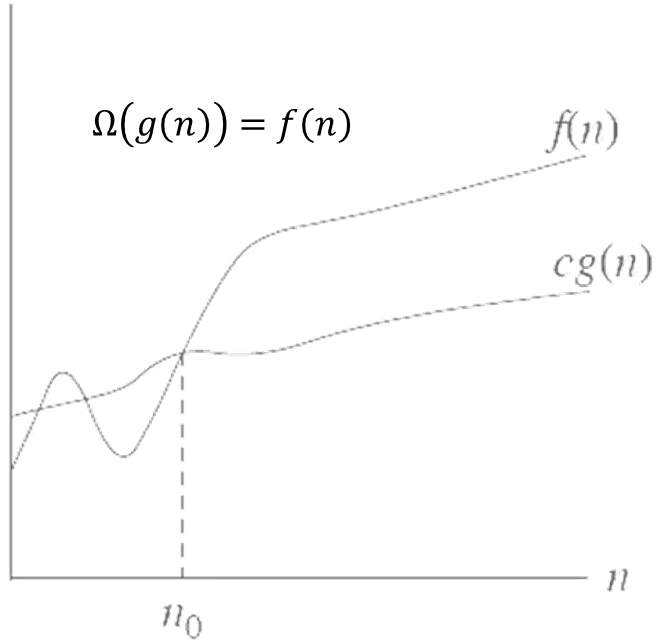
간단히 정리하면 다음과 같은 내용이다.
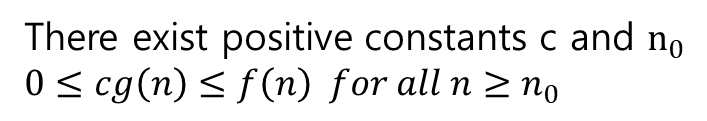
이젠 이해가 될거라 믿는다.
▷ Θ-notation
- 마찬가지로 살펴보자.
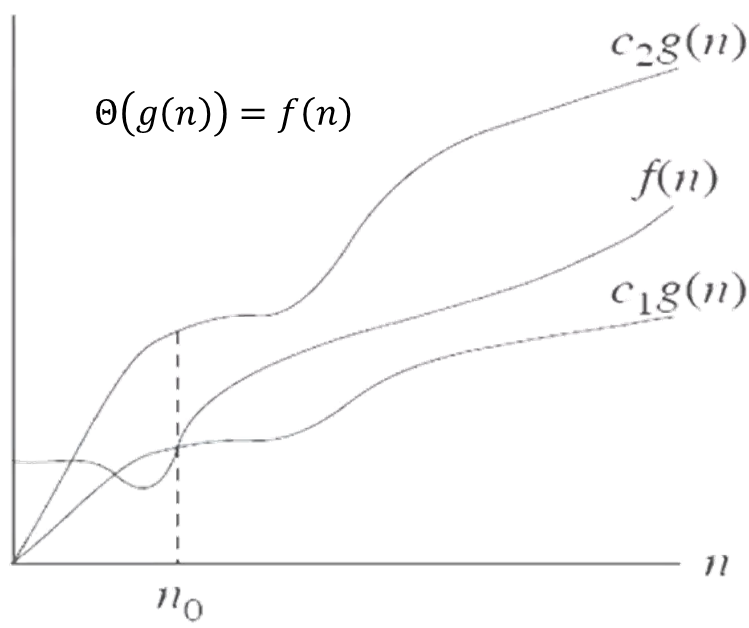
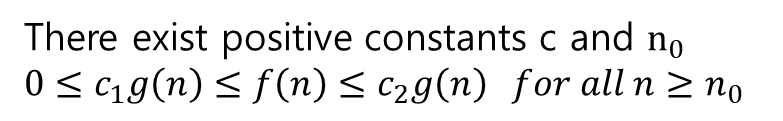
앞에서 공부한 Insertion Sort에 대해서 표기를 해보면 다음과 같다.
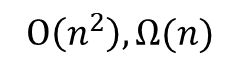
Best-Case / Worst-Case가 존재 하므로 Θ-notation은 없고,
O-notaion과 Ω-notation이 존재하고 각각의 값은 위와 같다.
나름 쉽게 정리해본다고 했는데.... 기회가 되면 F2F로 설명을 ^^
'Programming > Algorithm' 카테고리의 다른 글
| 알고리즘 #1 - 정렬 문제 #4 - Heap Sort #1 (0) | 2024.01.20 |
|---|---|
| 알고리즘 #1 - 정렬 문제 #3 - Merge Sort #1 (0) | 2024.01.06 |
| 알고리즘 #1 - 정렬 문제 #1 - Insertion Sort #2 (0) | 2023.12.10 |
| 알고리즘 #1 - 정렬 문제 #1 - Insertion Sort #1 (0) | 2023.11.27 |
| Base64 인코딩, 디코딩 (0) | 2023.11.12 |
