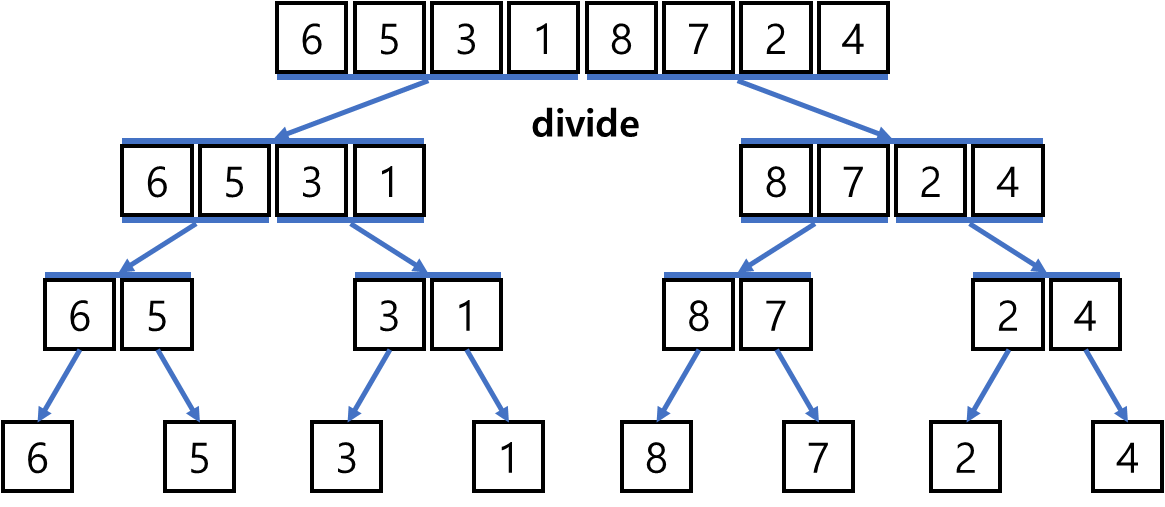
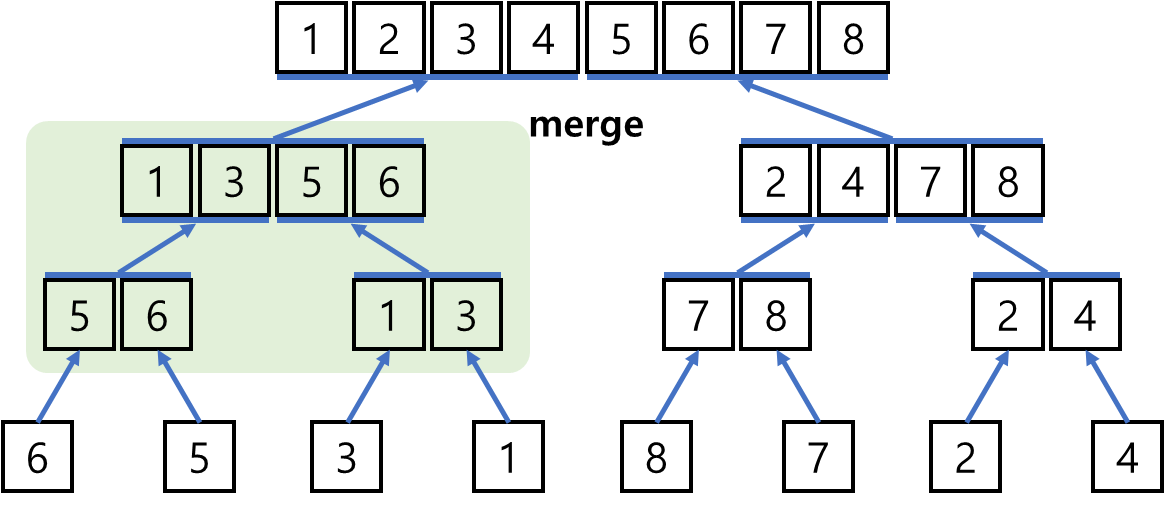
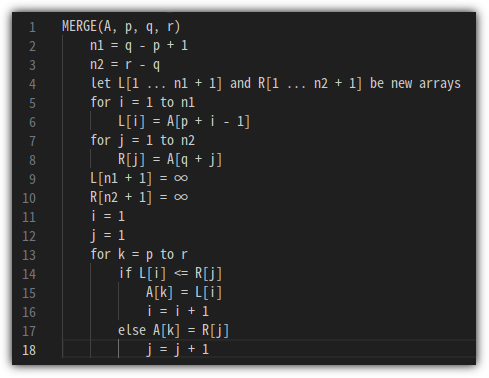
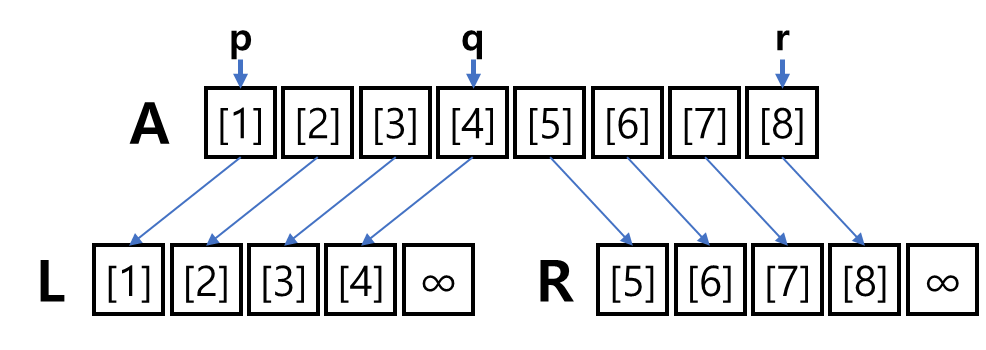
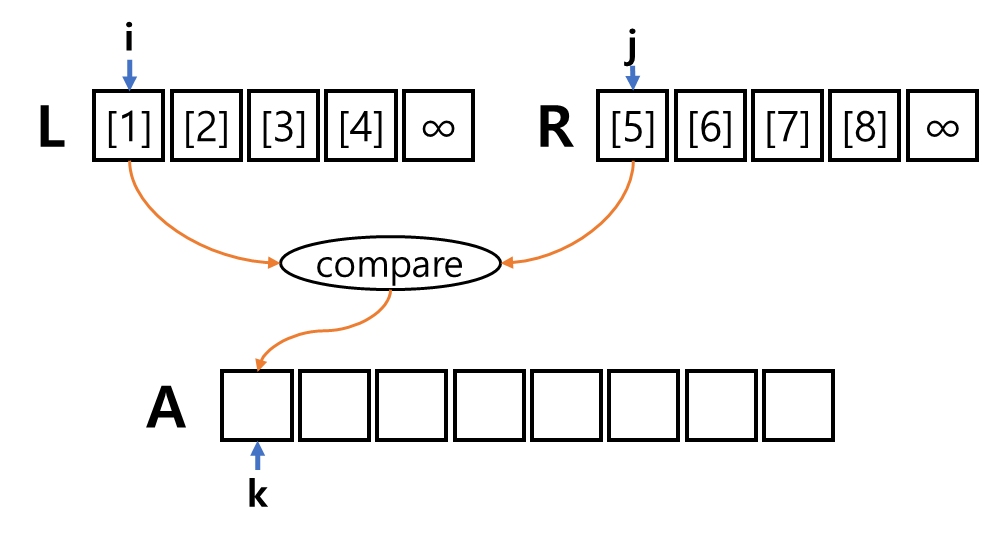
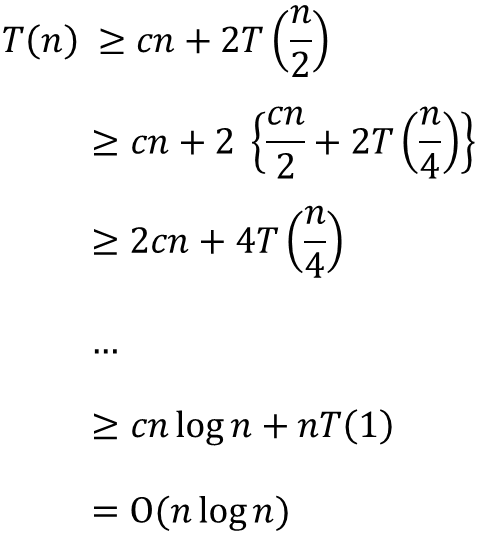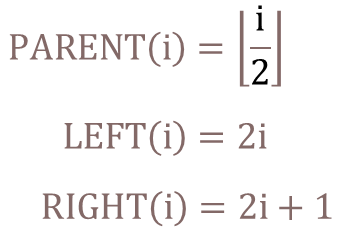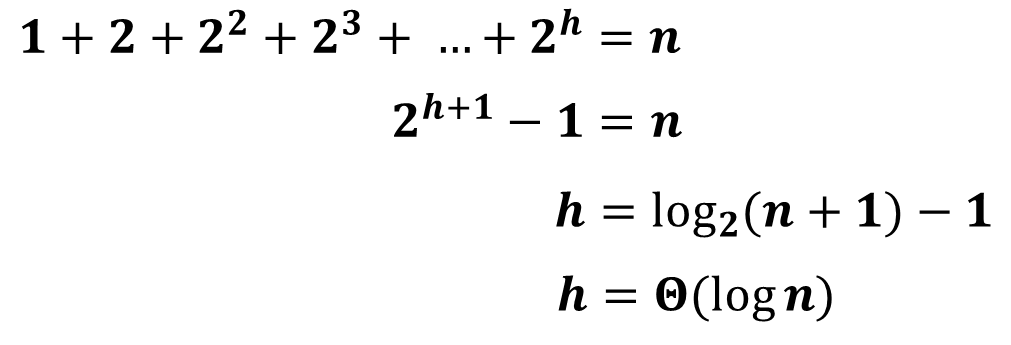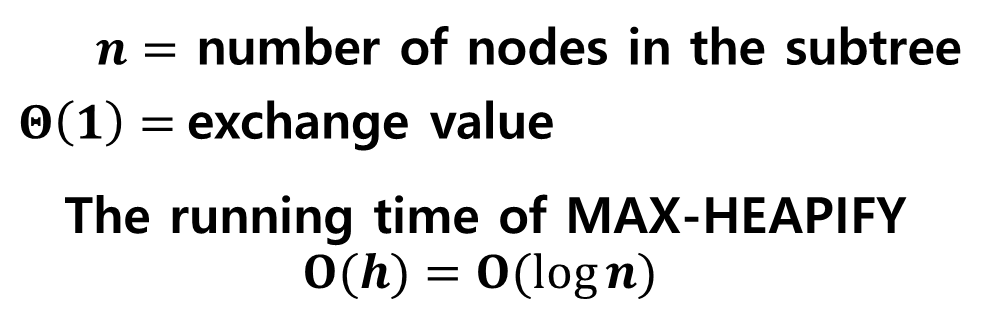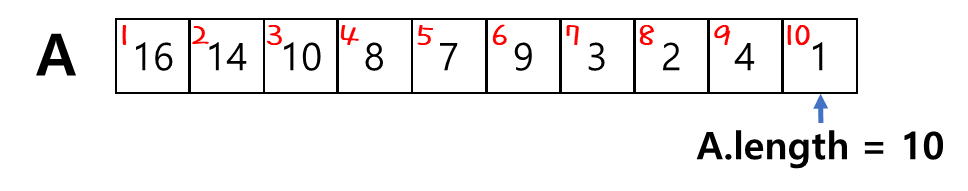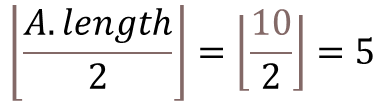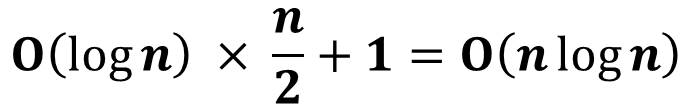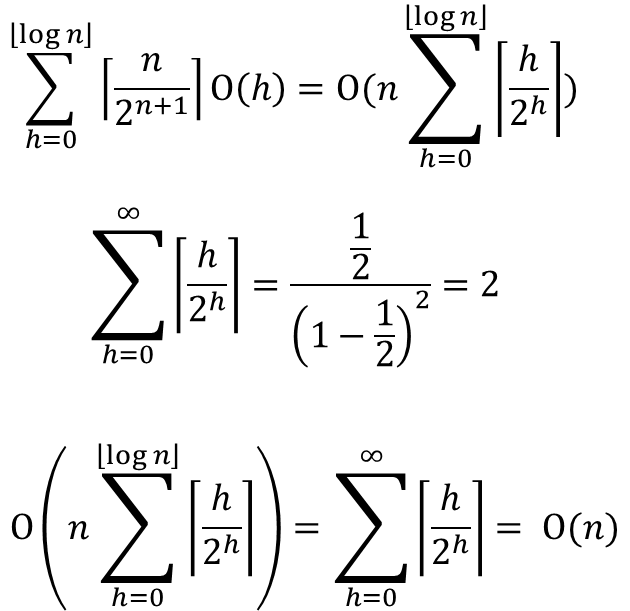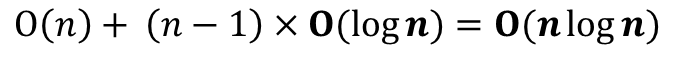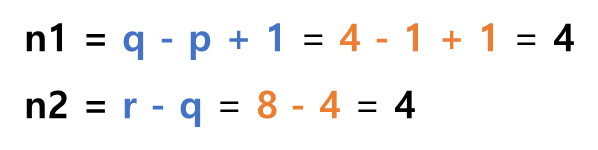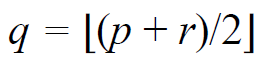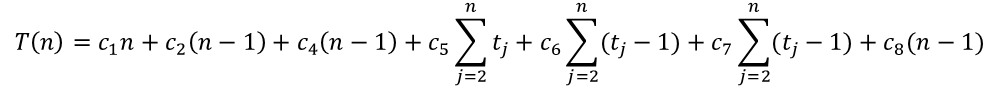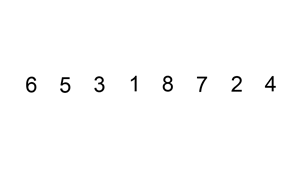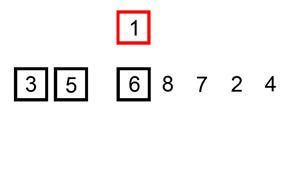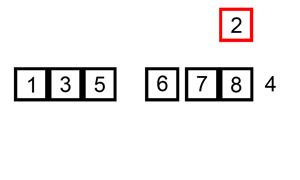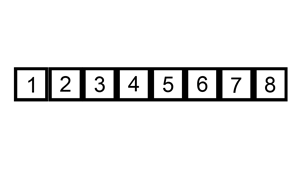이번에 살펴볼 정렬 알고리즘은 "Heap Sort(힙 정렬)"이다.
 [출처] ChatGPT + WHATWANT
[출처] ChatGPT + WHATWANT
보통은 위키피디아의 animated-gif 를 통해서 정렬 알고리즘을 엿볼 수 있었는데,
heap-sort 경우에는 도저히 파악이 안되는 내용이라 다른 자료를 찾아봤다. (내가 무지해서 이해를 못한 것이겠지...)
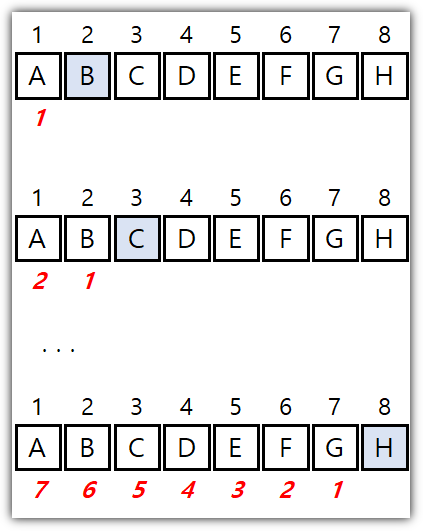
 [출처] https://www.cs.usfca.edu/~galles/visualization/HeapSort.html
[출처] https://www.cs.usfca.edu/~galles/visualization/HeapSort.html
너무나 친절한 Visualization을 제공해주는 곳은 다음과 같다.
- https://www.cs.usfca.edu/~galles/visualization/HeapSort.html
- 왼쪽 상단의 "Heap Sort" 버튼을 클릭하면 animation을 보여준다.
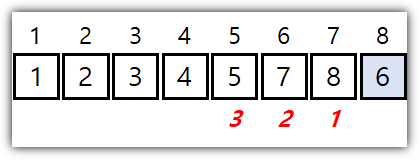
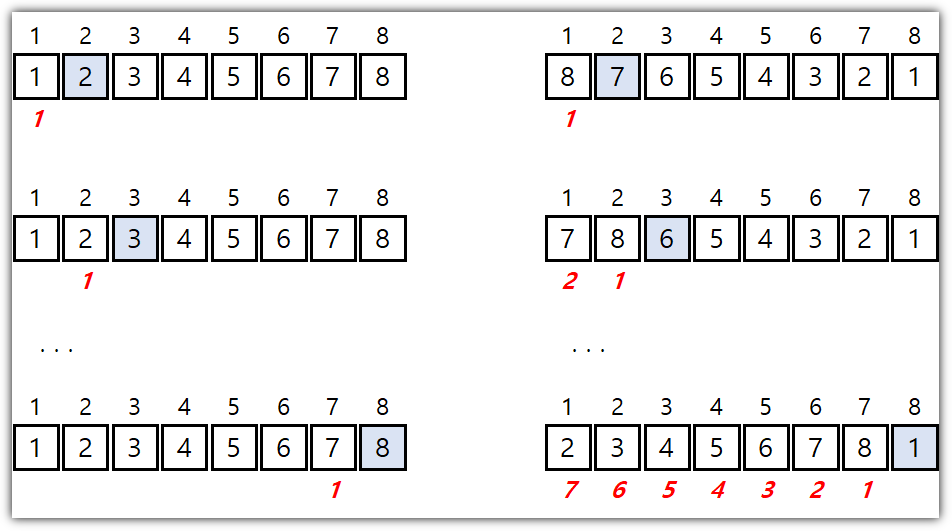
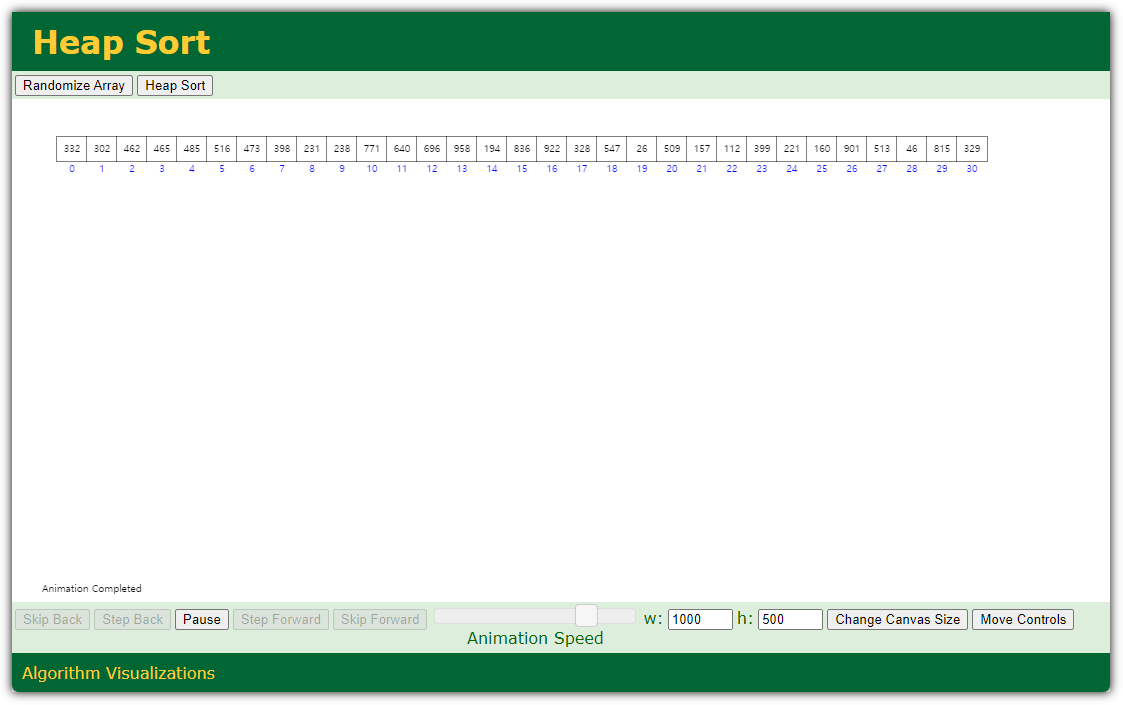 [출처] https://www.cs.usfca.edu/~galles/visualization/HeapSort.html
[출처] https://www.cs.usfca.edu/~galles/visualization/HeapSort.html
왜 저렇게 정렬이 되는지 바로 이해가 되시는 분은 그만 공부하셔도 된다!!! ^^
사실 공부하기 전에는 대체 어떤 이유로 이렇게 움직이는 것인지 잘 보이지 않아야 정상일 것 같다 ^^
우리에게 필요한건?
공부!!!
Heap Sort를 알기 위해서는 일단 Heap이 무엇인지 부터 알아야 한다.
⑴ Heap의 정의
⑵ MAX-HEAPIFY()
⑶ BUILD-MAX-HEAP()
⑷ HEAP-SORT
⑴ Heap
Heap은 2가지의 속성을 갖고 있다. 이에 대해서 알아보자.
① A nearly complete binary tree
② max-heap
① A nearly complete binary tree
일단 tree 구조와 관련한 용어부터 확인해야 이야기가 쉬울 것 같다.
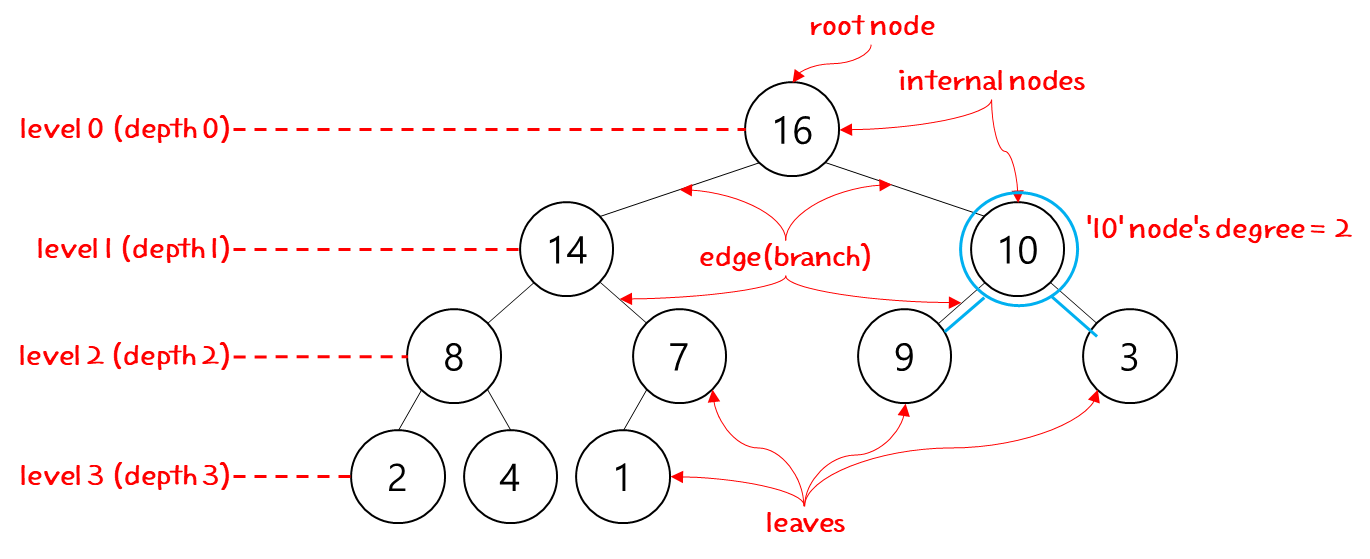 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
tree 관련한 용어들이 더 있지만, 일단 이 정도만 알아도 될 것 같다.
그러면, tree 구조 관련하여 "complete binary tree"가 뭔지부터 파악하고
"nearly complete binary tree"가 뭔지 이해해보도록 하자.
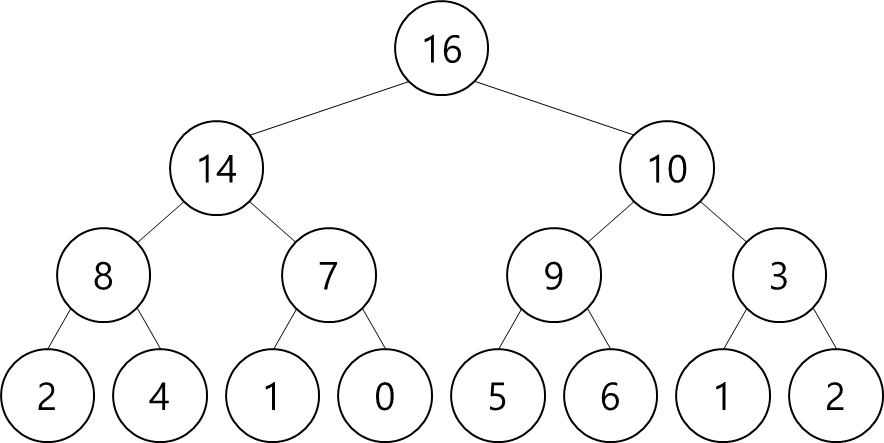 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
▷ Complete Binary Tree
- all leaves the same depth
- all internal nodes have degree 2
그러면 nearly complete binary tree는 어떻게 생겼을까!?
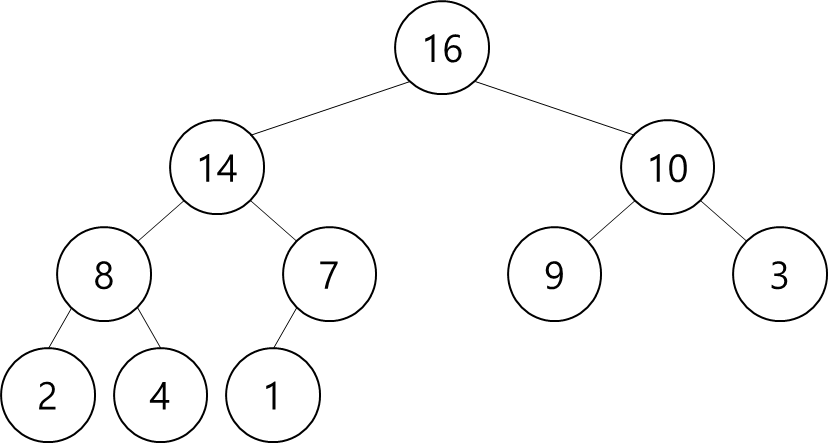 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
▷ A Nearly Complete Binary Tree
- 기본적으로는 Complete Binary Tree 구조를 갖고자
- all internal nodes have degree 2, but 마지막 leaf는 1개가 부족할 수 있다.
- 마지막 depth의 leaves는 왼쪽부터 차례대로 배치
우리가 공부하고자 하는 Heap 구조는 바로 이 "nearly complete binary tree"를 따르고 있다.
왜 그럴까!?
▷ Array
"nearly complete binary tree" 구조를 따를 경우에 이를 array 방식으로 표현하기가 쉽기 때문이다.
반대로 말하면 array를 사용하기 위해서는 nearly complete binary tree 구조여야 한다!!!
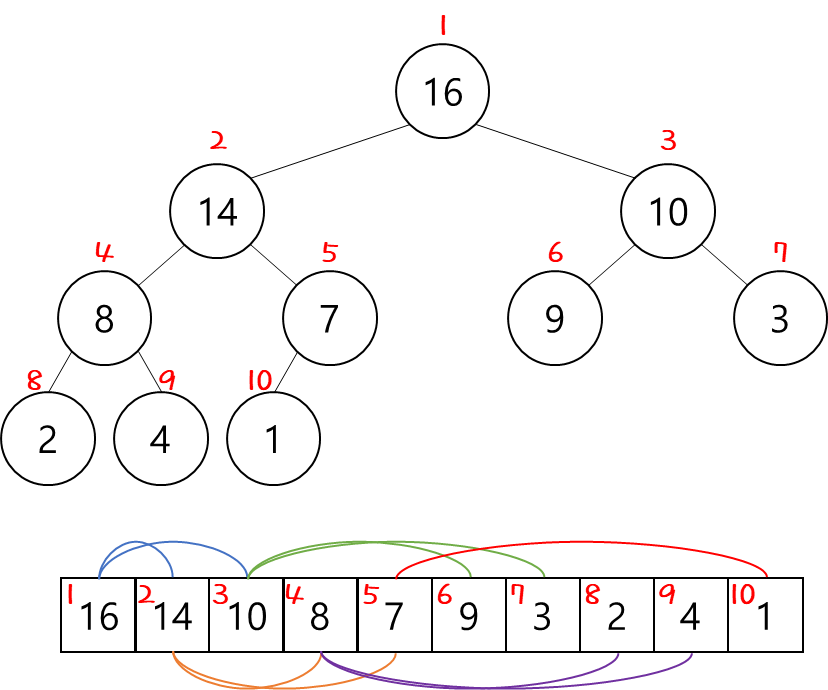 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
이렇게 되면 어떤 장점이 있을까?
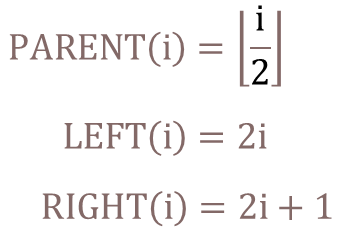 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
그렇다 ! 위치에 대한 계산이 가능해진다 !!!
여기에서 하나 더 확인해볼 것은 "The height of a heap"이다.
▷ The height of a heap
- 기본적으로 height는 depth와 같은 개념이고, 특정 node를 기준으로 depth가 얼마인지를 의미한다.
- The height of a heap = The height of the root : 그러면 depth의 의미이다.
- 그러면, 여기에서 질문 하나
: 어떤 Heap의 전체 node의 갯수(n)를 알면 height가 얼마인지 알 수 있을까?
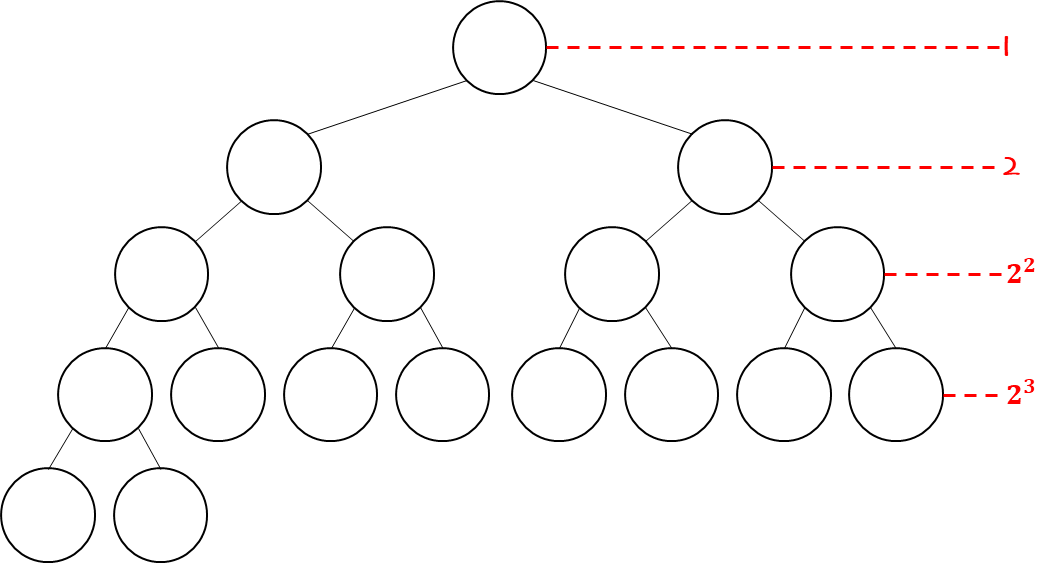 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
- height를 h라고 하면, 다음과 같다.
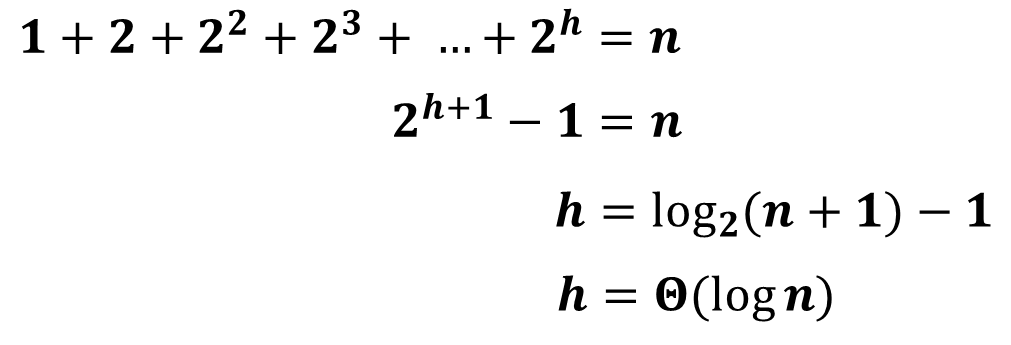 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
② max-heap
'binary heap'은 max-heaps와 min-heaps의 2가지 종류가 있다.
앞에서는 tree 구조에 대해서만 이야기 했지, 각 node에 들어있는 값에 대해서 이야기하지 않았다.
이제는 각 node에 들어있는 값에 대한 이야기이다.
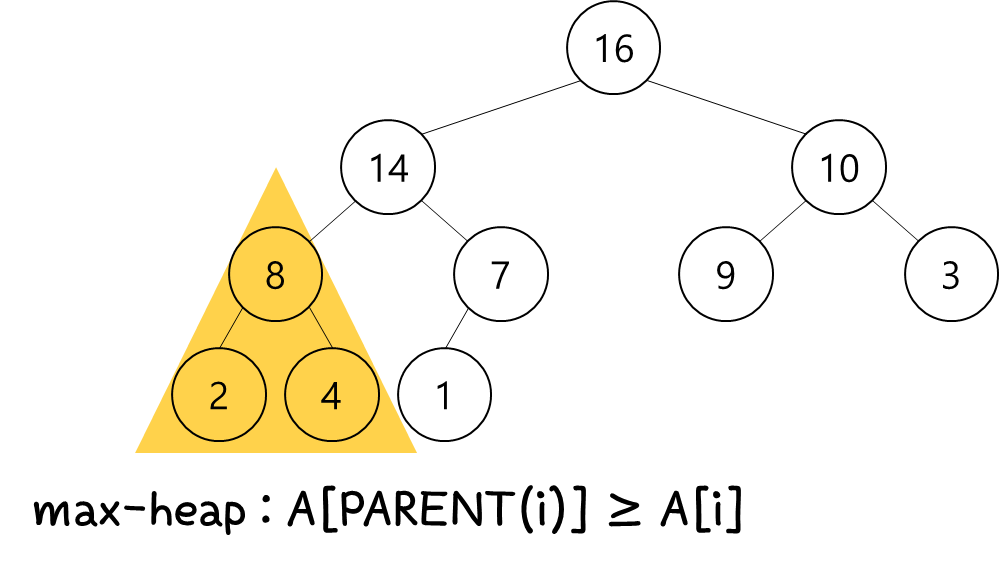 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
위 그림을 보고 오해를 하면 안된다.
당연하게도 모든 parent-child 를 살펴봐도 모두 저 관계를 만족해야 한다.
그러면 제일 위의 root node에 들어있는 값은 전체 모든 node 중에서 가장 큰 값이 위치하게 된다.
min-heap은 반대이다. root node가 가장 작은 값을 갖는다.
우리는 보통 max-heap을 사용한다.
⑵ MAX-HEAPIFY()
"Max-Heapify" 함수에 대해서 알아보겠다.
함수이기에 입력(input)과 출력(output)이 있고, 그 과정에서 어떤 처리(processing)이 있을 것이다.
① input
- 입력은 어떤 하나의 node가 된다.
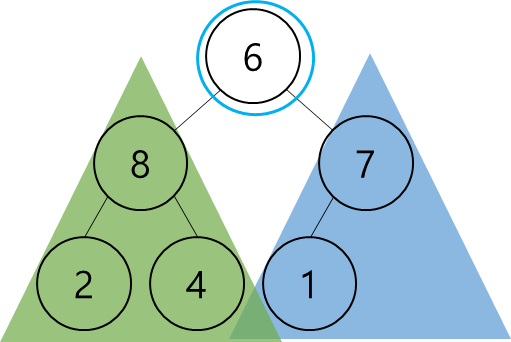 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
- 단, 그 노드가 갖고 있는 왼쪽/오른쪽의 subtree들이 이미 max-heap 구조를 갖고 있어야 한다.
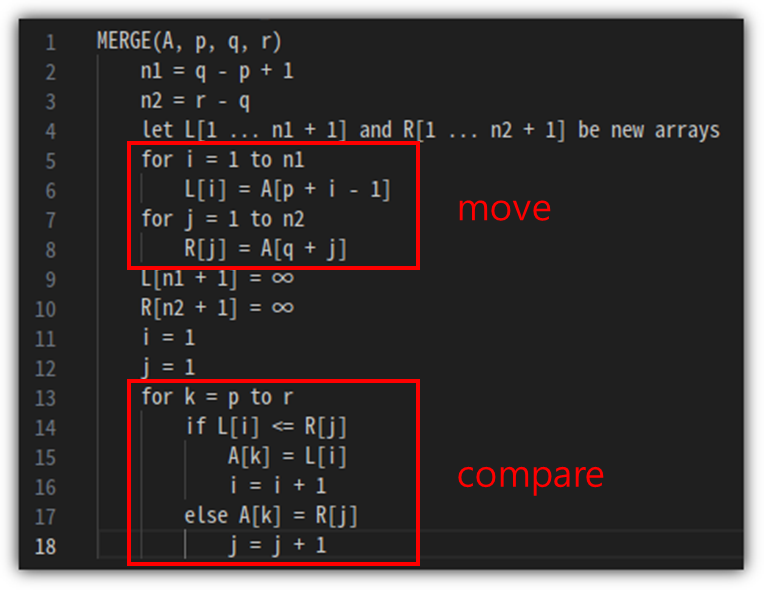
② float down
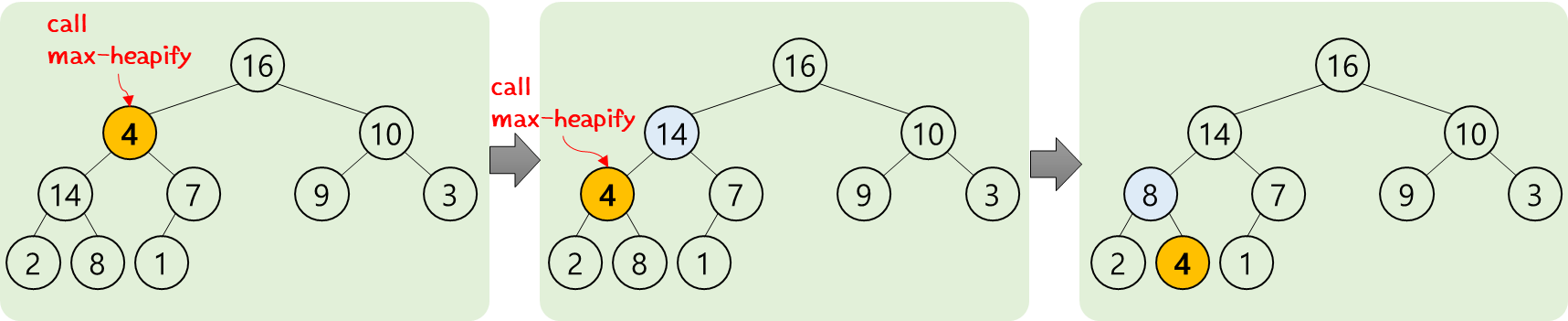
- "4" node를 기준으로 왼쪽/오른쪽 subtree가 각각 max-heap이기에 max-heapify 가능
- 그래서 "4" 값과 "14"값을 exchange
- 그런데, "4" node를 봤더니 max-heap 상태가 아님
- subtree 들은 각각 max-heap 상태이기에 max-heapify 실행
- 그래서 "4"와 "8"값 exchange
- 그랬더니, 처음 "4"에서 실행한 max-heapify가 전체적으로 이루어짐
 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
이렇게 밑으로 흘러가듯이 이루어지는 과정을 "float down"이라고
③ running time
- max-heapify의 running time을 알아보자.
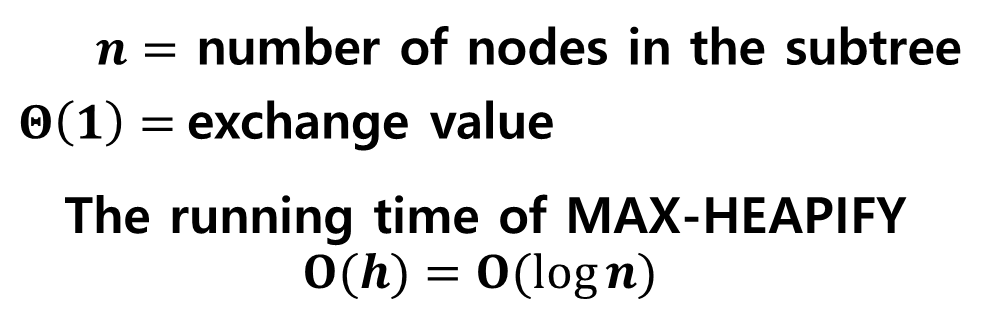 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
⑶ BUILD-MAX-HEAP()
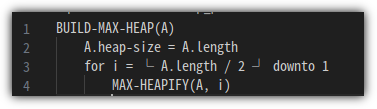
max-heap을 만드는 것에 대한 Pseudo Code를 살펴봅시다!!!
 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
Text에서 floor 함수 표기가 쉽지 않아 조금 이상하게 보이는 부분은 이해해주시길 바라옵니다 ^^
일단 A는 max-heap을 하고자 하는 입력 데이터를 의미한다.
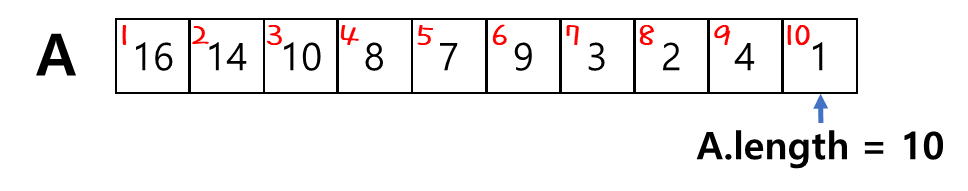 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
그러면, 밑의 순환문은 어떤 의미일까!?
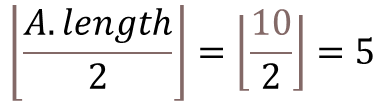 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
그러므로, 순환문의 시작 위치는 다음과 같다.
 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
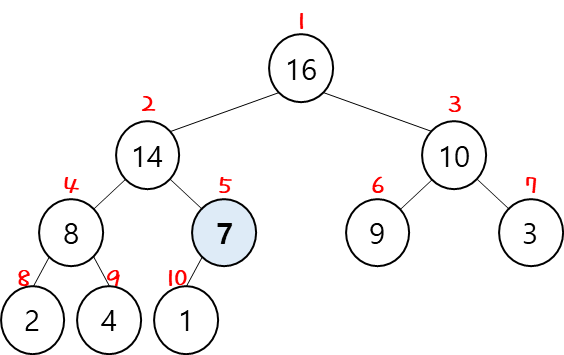
그 다음 index가 하나씩 감소하기 때문에 다음과 같은 흐름으로 진행하게 된다.
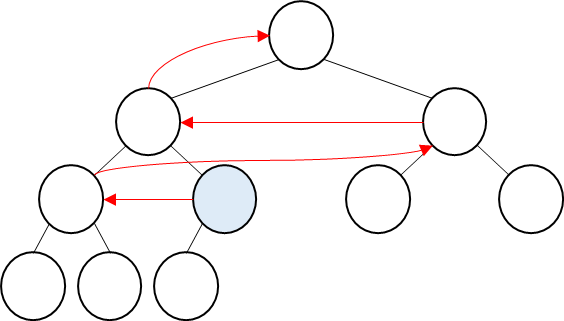 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
전체 길이의 절반 위치에서 시작하는 것은 그 이후의 node는 edge-node 즉, leaves 들이기 때문에
이미 max-heapify가 되어 있어서 굳이 max-heapify를 할 필요가 없는 것이다.
▷ Running time
① Upper bound
- Pseudo code를 기반으로 해서 찬찬히 살펴보면 다음과 같이 실행 시간(횟수)를 확인할 수 있다.
 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
이를 계산하면 다음과 같이 정리가 된다.
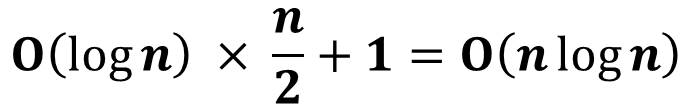 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
② Tighter bound
그런데, 실제로 분석해보면 이는 지나친 upper-bound라고 볼 수 있다.
즉, 이것 보다는 조금 더 tighter-bound를 계산해볼 수 있는 것이다.
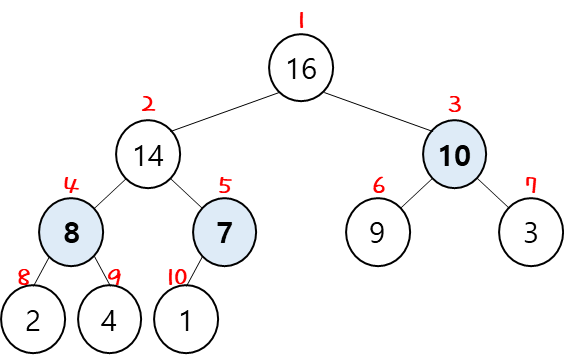
1번 node 기준으로 max-heapify를 한다고 했을 때, "n = 10" 이므로 O(log 10) 소요시간이 걸린다.
그러면, 5번 node 기준으로 max-heapify를 하면 소요시간이 얼마나 걸릴까?
 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
5번 node 위치에서의 "n = 2" 이므로 O(log 2) 소요시간이 걸린다.
4번 node 위치에서는 O(log 3), 3번 node 위치에서도 O(log 3) 이다.
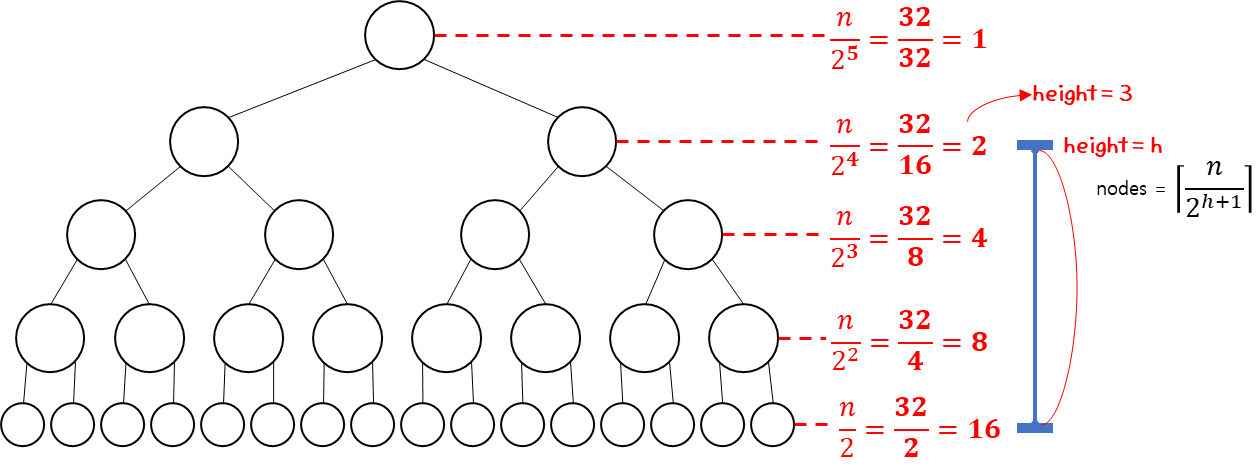
즉, 실제로 많은 node에서 소요되는 시간이 우리가 계산한 O(log n) 값보다 작다는 것이다.
 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
이걸 고려해서 계산을 해보면 다음과 같다.
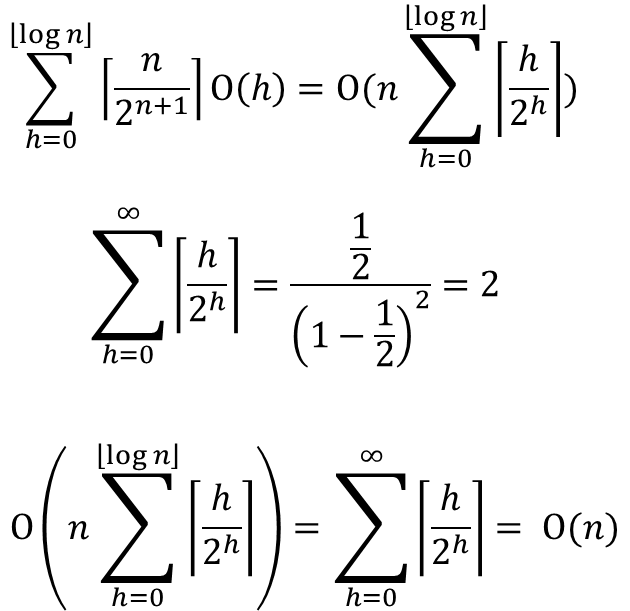 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
엇?! 선형(linear)으로 정리가 되었다 !!!
⑷ HEAP-SORT
이제 마무리 단계에 왔다.
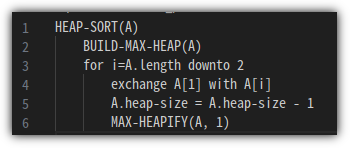
앞에서 공부한 것들을 모두 모아서 정렬하는데에 어떻게 사용할 수 있는지 Pseudo Code로 살펴보자.
 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
응!? 이건 뭔가 싶다.
▷ Extract-Max
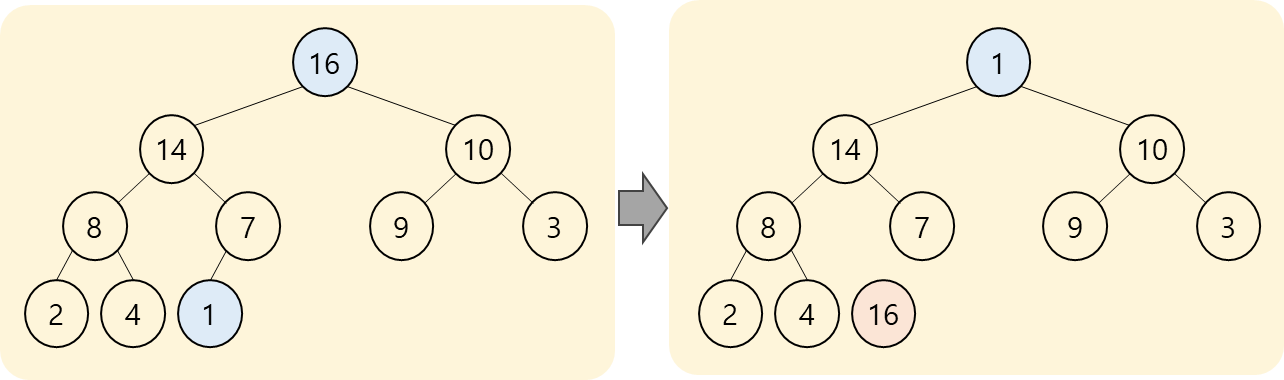
- BUILD-MAX-HEAP() 실행을 마치면, root-node에 있는 값이 가장 큰 값이 되게 된다.
 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
- root-node에 있는 값을 제일 뒤에 있는 node와 교환을 한다.
- 제일 뒤에 있는 node를 제외한 tree를 가지고, root-node에서 MAX-HEAPFY()를 실행한다.
- 이 방식 가능한 이유는 이미 BUILD-MAX-HEAP()을 통해, 그 밑의 subtree들이 max-heap 상태이기 때문이다.
▷ Running Time
- Pseudo Code를 가지고 수행 시간을 살펴보자.
 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
- Worst-case는 이렇게 되겠지만, Best-case는? 모든 것이 같은 값일 때 !!!
- 5번 라인의 경우 값이 하나씩 줄어들기 때문에, 시간이 조금씩 더 적게 들겠지만 유의미하지는 않다.
- 결론적으로 Heap-Sort의 Running Time은 다음과 같이 정리할 수 있다.
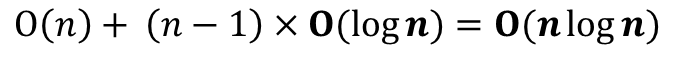 [출처] https://www.whatwant.com
[출처] https://www.whatwant.com
▷ Memory
- Heap-Sort는 추가적인 메모리가 필요하지 않은 in-place 알고리즘이다.
- 별도의 메모리 공간이 아니라 node 사이의 값을 exchange하는 것으로 처리되기 때문이다.
우아앙~ 너무 힘들었다.