cron에 대해서 그동안 한 번쯤은 포스팅 했을 줄 알았는데, 찾아보니 없어서 이번 기회에 한 번 정리해본다!
cron
- 주기적으로 실행해야 하는 작업(task)을 관리하기 위한 시간 기반 잡-스케줄러(Job Scheduler)
- 사용자들은 crontab 파일을 사용하여 특정 시간에 특정 명령이나 스크립트를 실행하도록 설정
- 시스템 유지보수 작업, 데이터 백업, 로그 분석 등 다양한 자동화 작업을 주기적으로 수행하는 데 사용
Linux 사용자라면 누구나 알고 있지만, 의외로 누구나 사용하지는 않는/못하는 도구이다 !!!
Unix 계열이라면 어디에나 존재하고 있는 시간 기반의 잡-스케줄러이고,
아주 기본이 되는 도구이다보니 이를 기반으로 동작하는 다른 유틸리티도 다양하게 존재하고 있다.
Etymology(어원)
"cron"이라는 명칭은 어디에서 비롯되었을까?
- 그리스 신화에서 "시간의 본질"을 상징하는 신 "Chronos"에서 비롯되었다고 한다.
. https://en.wikipedia.org/wiki/Cron
. 왠지 시계 관련하여 많이 들어본 이름인 것 같다~

History (역사)
- 시작은 1975년 그 유명한 "AT&T Bell 연구소"에서 탄생되었다고 한다.
- Linux의 등장과 함께 다양한 cron alternative들이 등장하게 되는데
- 현재 가장 널리 퍼진 것은 1987년에 탄생된 vixie-cron 이라고 한다.
. https://github.com/vixie/cron

- Red Hat에서 vixie-cron 4.1을 fork해서 만든 cronie 프로젝트도 있고,
. https://github.com/cronie-crond/cronie
- vixie-cron과의 호환성을 보여주는 mcron 프로젝트도 있다.
. https://github.com/Dale-M/mcron
Check
이번 포스팅을 작성하는 환경은 "Ubuntu 20.04.6 LTS" 이다.
다른 환경에서도 얼추 비슷하지 않을까 하지만, 혹시라도 다른 결과가 나올 수도 있다는 점은 유념 !!!
- 패키지 설치 여부
. dpkg -l | grep cron
- 실행파일 위치
. which cron
- 서비스 상태
. systemctl status cron

crontab
- "cron table"의 약자로써, cron 데몬이 실행해야할 작업들의 스케줄을 정의한 테이블을 의미한다.
- 테이블을 작성/수정할 수 있도록 해주는 유틸리티 명칭이기도 하다.
- 첫 실행을 하면 어떤 에디터를 사용할 것인지 물어본다.
. 개인적으로 애용하는 nano 에디터를 추천해줘서 더 반갑다!!! ^^

- 정확히 표현하자면, 현재 사용하는 계정에서 처음 실행할 때 기본 에디터를 설정해주는 것이다.

- 각 계정별로 하나의 (cron) table이 주어진다.
- 간단한 가이드를 주석(#)에서 확인할 수 있다.
- cron 관련해서 항상 우리를 괴롭히는 익숙하지 않은 시간 표현 순서 !!!

- dom : day of month
- dow : day of week
- 잘 동작하는지 한 번 테스트 해보자.

- 이미 알고 있겠지만, " * "는 every를 의미한다. 즉, 매분마다 환경변수들을 /tmp/env.output에 저장하게 된다.

Seperator (구분자)
정보를 입력할 때 각 값들을 구분하기 위해서 기본적으로 space 한 칸을 사용했을 것이다.
만약 space 두 칸을 사용해도 괜찮을까? 괜찮다! 여러개의 space를 사용해도 잘 인식한다.
심지어 tab을 사용해도 된다 !!!
Represent (표현식)
- 기본적인 내역은 다음과 같다.
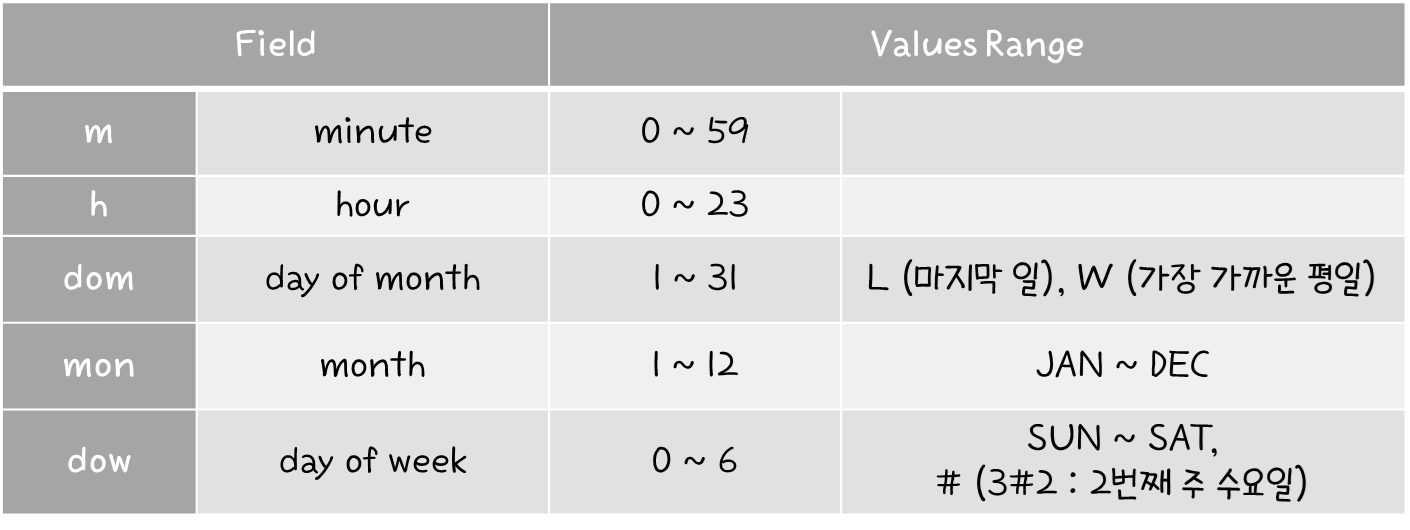
- 특수 문자들은 다음과 같다.
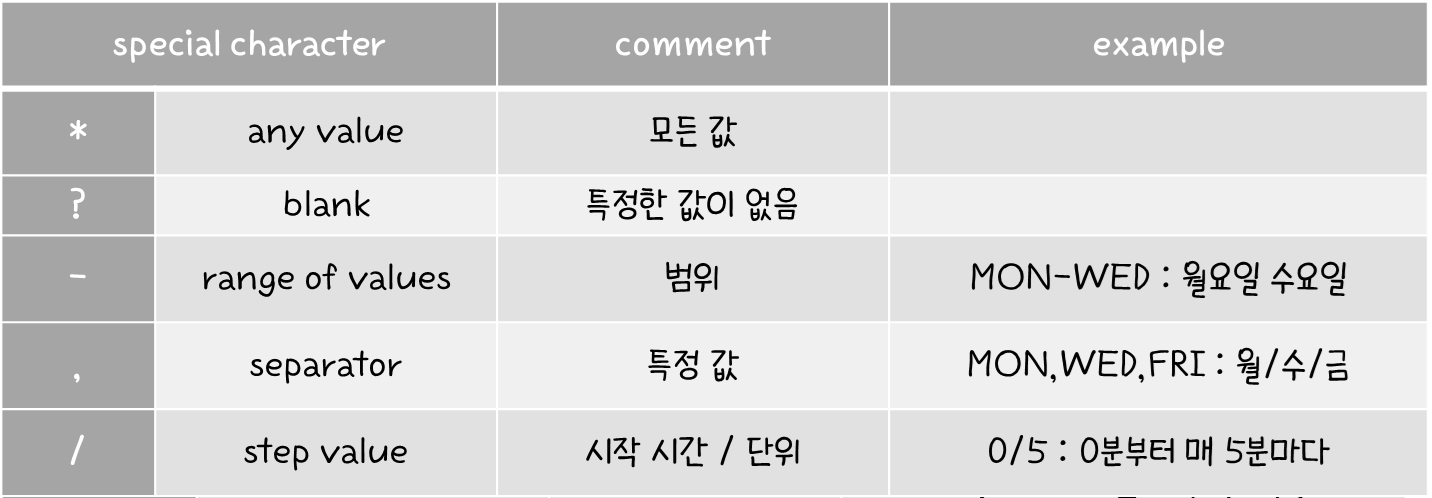
Example (예시)
몇 가지 사례를 들어보자. ( "?"는 사실 낚시성일까나..... ㅋㅋ )

- 매일 오전 10시 15분에~

- 매일 오후 3시에 시작해서 5분마다 실행되어 오후 3시 55분에 끝나고,
다시 오후 7시에 시작해서 5분마다 실행되어 오후 7시 55분에 끝남

- 매일 00시 30분부터 6시간 마다 실행 (00:30, 06:30, 12:30, 18:30)

- 평일(월요일~금요일) 1시 30분 부터 매 6시간 마다 실행 (01:30, 07:30, 13:30, 19:30)
Log
Ubuntu 환경에서 cron 로그를 위한 기본 경로는 "/var/log/cron.log" 이다. 하지만,

로그 기록을 활성화 시켜줘야 한다.

주석 처리 되어 있는 cron 부분을 확인 후, 주석 제거하고 저장하면 된다.

서비스 적용을 위해 rsyslog 재시작을 한 번 해주면 된다.

이제 cron이 잘 동작했는지 확인할 수 있는 로그를 볼 수 있게 되었다.

Remove (삭제)
현재 crontab 내역을 확인하고 싶으면 "-l" 옵션을 사용할 수 있다.
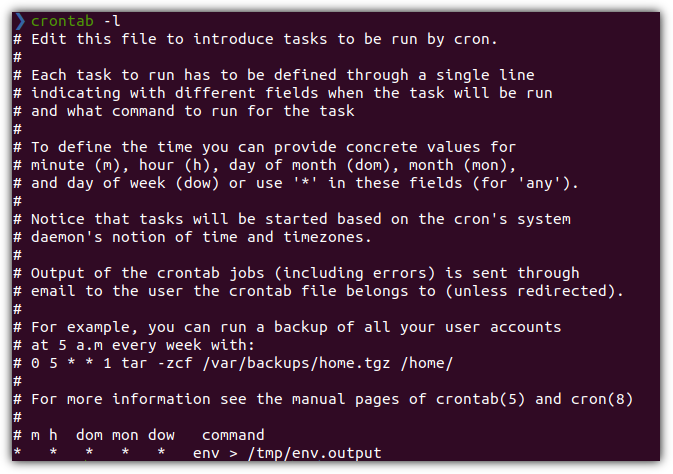
전체 내용을 삭제하고 싶다면, "-r" 옵션을 사용할 수 있다.

특정 스케줄만 삭제하고 싶다면? "-e" 옵션으로 편집 화면에서 해당 라인을 삭제하면 된다 !!!
Helper (도우미)
① CronTool (https://tool.crontap.com/cronjob-debugger)
- 오른쪽 하단위 Cheetsheet를 보면 hour 부분에 Values Range 오타가 조금 아쉽긴 하지만,

- 깔끔한 화면과 함께, 달력으로 설정 내역을 보여주는 것이 정말 괜찮다.

② Cronitor (https://crontab.guru/)
- 정말 simple하고 URL 주소를 외우기도 쉽다.

③ CronMaker (http://www.cronmaker.com/?1)
- 원하는 cron 표현식을 쉽게 만들 수 있도록 편리한 인터페이스를 제공해주고 있다.
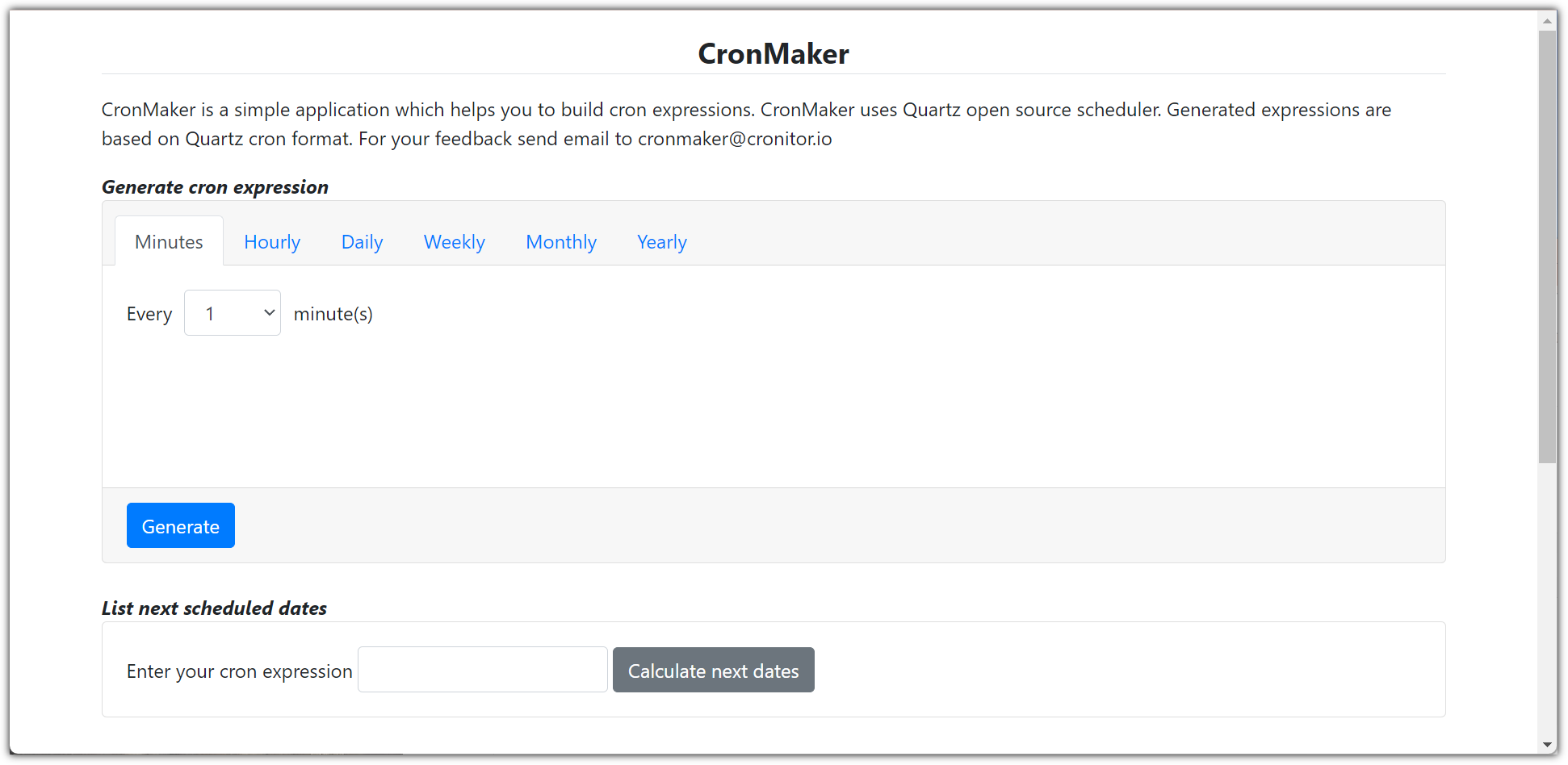
지금까지 살펴본 내용 외에도 더 많은 것들이 남아있다.
cron의 세계는 의외로 넓다 !!
하지만, 한 번에 너무 많은 것을 알게 되면 다칠 수 있으므로(?) 여기에서 일단 마무리 해보련다 !!!
절대 지쳐서 그런 것 아니다! (그런가? ^^)
'OS > Ubuntu' 카테고리의 다른 글
| 커맨드-라인 명령어를 쉽게 사용하기 - fzf (0) | 2024.11.17 |
|---|---|
| 서버야! 얼마나 힘드니? - Load Average (0) | 2023.07.15 |
| 더미 파일 만들기 (fallocate, truncate) (0) | 2023.06.28 |
| Ubuntu Server 22.04 LTS 설치 (0) | 2023.04.15 |
| 리눅스 원격데스크탑 (ubuntu 18.04 - vino) (2) | 2022.03.20 |